7.2
7.3
7.3.1The Chain Rule as Substitution in Differentials
7.4
Example CD-7.1
The Fast Lighthouse
A lighthouse is 1 mile off a straight shore with its beacon revolving 3 times per minute.
How fast does the beam of light sweep down the beach at the points that are 2 miles from the point closest to the lighthouse?
The "chain" in this exercise is that the angle of the beacon depends on time and the distance to the point of contact down the beach depends on the angle.
We will assume that the light revolves clockwise in the diagram Figure CD-7.1. We want to know the rate of change of distance with respect to time.
We introduce the variables shown in the diagram Figure CD-7.1:
The link between the angle and the distance is
The link between the time and the angle can be expressed as an explicit function, but what is important is to know the rate of change,
The question in this problem is
SOLUTION: Distance as an explicit function of time is
This formula tells us the speed of the light's motion in terms of
The specific position when D=2 is shown in Figure CD-7.2.
The Pythagorean Theorem applied to Figure CD-7.2 tells us that the hypotenuse of the right triangle shown is
Finally, when D=2
Example CD-7.2
The Lightspeed Lighthouse
The beam of light in the previous example moves down the beach faster and faster, but real light can only move at the speed of light.
The Scientific Project on the Lightspeed Lighthouse examines the example taking into account that the light must travel from the lighthouse to the shore at the speed of light.
7.5
Example CD-7.3
Implicit Solution of Exercise CD-7.1
After you solve Exercise CD-7.1, you should compare your solution to the following implicit method.
We begin with the equation
The total differential of the equation is
When (a,b,c)=(1,-2,1), the only root of the original equation is x=1. In this case, the implicit differential breaks down
Of course, this degeneracy is only a hint of the trouble in the original implicit equation.
If we change b to -1.99, there are no real solutions to the original problem.
The equation "branches" here between the positive discriminant and negative one,
Differentiating the explicit function x[b] is more complicated, as you saw in Exercise CD-7.1:
Example CD-7.4
Implicit Solution of the Balloon Exercise CD-7.5.1
In Exercise CD-7.5.1, you calculate the rate of change of surface area of a balloon that is being blown up so that its volume is increasing at the rate of 2 cubic inches per second.
We want to know how the rate of change of volume effects the rate of change of surface area.
In the exercise, we ask you to solve explicitly for surface area as a function of volume.
The implicit solution of that problem does not require that we find the explicit function.
Here is the implicit solution of the problem:
We solve the volume differential for dr,
Example CD-7.5
The Fast Ladder
A ladder of length L rests against a vertical wall.
The bottom of the ladder is pulled out horizontally at a constant rate r (m/sec). What is the vertical speed of the tip that rests against the wall? We introduce the variables shown in Figure CD-7.4:
The fact that the length of the ladder is fixed together with the Pythagorean Theorem gives us the implicit linkage between x and y:
The total differential of the implicit equation is
Example CD-7.6
A Limiting Case
As we pull the base of the ladder toward the point x=L away from the wall, what happens to the speed with which the other tip moves down the wall? We can see from the diagram, Figure CD-7.5, that when
Humm, this calculation is a little mysterious.
Here is another way to look at it: Solve the equation x2+y2=L2 for
HINTS: Give variables for surface area, volume, time, and whatever else you need.
Solve for S in terms of V. The "chain" in this exercise is that volume depends on time (through the child's efforts), V=V[t] and surface area depends on volume, S=S[V]. We want to know how area changes with time,
The result of the previous exercise is wrong for a real ladder.
The tip of such a ladder cannot go faster than the speed of light.
There is a physical condition that this simple mathematical model does not take into account.
The real falling ladder is explored in the Scientific Projects Chapter on Mechanics.
It uses Galileo's Law of Gravity from Chapter 9.
7.6
7.3.2
Section Summary
Many applications of calculus involve different quantities that vary with time but are "linked" with one another; the time rate of change of one variable determines the time rate of change of the other.
This section illustrates the idea with examples including the falling ladder.

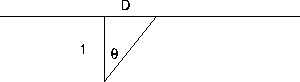
Figure CD-7.1: A lighthouse beam sweeps the shore
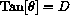
because D/1 is the opposite over the adjacent sides. (SOH-CAH-TOA).
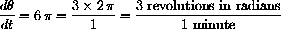
Because the derivative is constant, this is equivalent to
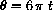 , because t=0 when
, because t=0 when
 .
.
FIND: 
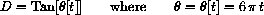
The Chain Rule gives us
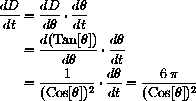
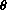 . Notice that
. Notice that
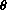 is not the independent variable t, but instead is the link variable or output from the first function in the chain.
We could use the first function
is not the independent variable t, but instead is the link variable or output from the first function in the chain.
We could use the first function
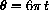 to express the speed in terms of t, but this is neither necessary nor desirable (unless we want to know when the light gets to the point 2 miles down the beach.) In fact, it is not even necessary to know the derivative
to express the speed in terms of t, but this is neither necessary nor desirable (unless we want to know when the light gets to the point 2 miles down the beach.) In fact, it is not even necessary to know the derivative
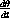 at any other time; it need not be constant as long as we know that
at any other time; it need not be constant as long as we know that
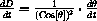 .
.
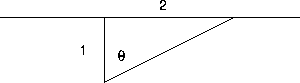
Figure CD-7.2: The angle when D=2  . SOH-CAH-TOA tells us that
. SOH-CAH-TOA tells us that
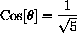
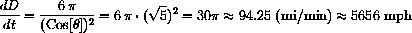
COMMON ERROR: A common error in related rate problems is to fix a quantity too soon.
In the example above, we want the speed
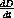 when D=2; but, if we fix this position at D=2 miles down the shore before we differentiate, we get
when D=2; but, if we fix this position at D=2 miles down the shore before we differentiate, we get
 so
so
 is constant and there is nothing to differentiate.
You must think about the drill problems in their general variable cases, differentiate, and then fix the quantities at the specific values.
is constant and there is nothing to differentiate.
You must think about the drill problems in their general variable cases, differentiate, and then fix the quantities at the specific values.
Section Summary
Implicit solutions of related rates problems often are simpler and more revealing than first solving for a quantity explicitly.
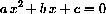
We are told that a and c are known exactly but that b is measured and may have some error when we determine the largest root x satisfying the equation above.
In other words, the independent variable b implicitly determines the variable x. The variables in this problem are b and x, and x is the dependent variable.
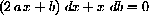
The first term is the familiar derivative with respect to x and the second is the derivative with respect to b, thereby treating all other letters, including x, as parameters.
The rate of change of x with respect to b is obtained by solving
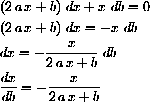
When (a,b,c)=(1,-3,2), the largest root of the original equation is x=2, so as b varies from -3, 
For example, if b+db=-3+.001=-2.99, then
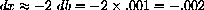 and x+dx=1.998. (The exact solution is
and x+dx=1.998. (The exact solution is
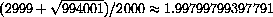 .)
.)

This equation cannot be solved for dx. Implicit differentiation of
 fails in this case.
We still can graph the line 0dx+db=0 in the (db,dx)-plane.
The equation db=0 is the vertical dx-axis, and vertical lines do not have slopes.
fails in this case.
We still can graph the line 0dx+db=0 in the (db,dx)-plane.
The equation db=0 is the vertical dx-axis, and vertical lines do not have slopes.
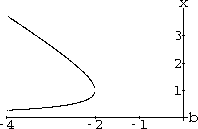
Figure CD-7.3: x2+bx+1=0 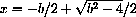 and
and
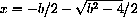 . The vertical tangent we just computed is the tangent touching these two branches shown in Figure CD-7.3.
. The vertical tangent we just computed is the tangent touching these two branches shown in Figure CD-7.3.
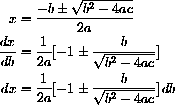
The implicit and explicit formulas for dx are the same when
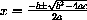 .
.

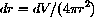 and substitute into the surface differential,
and substitute into the surface differential,
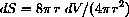 , obtaining
, obtaining
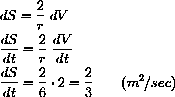
Compare this solution with your explicit solution from Exercise CD-7.5.1 that first solves
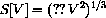
and uses the Chain Rule to compute

The length L is a parameter, fixed, but not known to us.
We wish to
FIND: 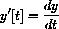
in terms of
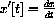 and the other variables.
and the other variables.
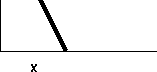
Figure CD-7.4: Ladder and wall
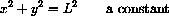
The fact that there is some implicit relationship is clear physically.
If we place the base of the ladder at a given x, we know that there is a unique place, y, where it will rest against the wall.
We could solve the equation above for y, since only the positive solution makes physical sense, but we will leave that approach to the problem to an exercise below.
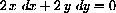
which we can solve for
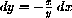 . In this problem, we also know that x and y are functions of time.
This means that the differentials can be expanded
. In this problem, we also know that x and y are functions of time.
This means that the differentials can be expanded

Substitution of the time expressions of the differentials into the equation above yields the solution to our question: 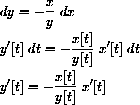
The time rate of change of y equals the time rate of change of x times x over y and the motion is down, or y'[t] is negative.
Suppose we have an enormous ladder of length 5 m.
If the base rests 3 meters from the corner, then y=4. If we are pulling the base out from the wall at the rate of 1/7 m/sec, then the top is moving down the wall at the rate

If the base of this same ladder is moved to 4 meters from the corner so that y=3 and if the base is still pulled out at the speed x'[t]=1/7, then the speed down the wall is
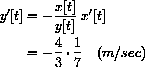
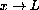 ,
, 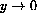 . The formula for the vertical speed tends to minus infinity.
. The formula for the vertical speed tends to minus infinity.
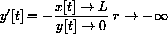
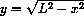 and substitute into the expression for vertical speed,
and substitute into the expression for vertical speed,
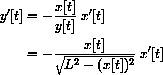
Clearly, as x tends to L, 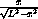 tends to infinity.
This is correct mathematically, and we want you to verify it in Exercise CD-7.5.2.
tends to infinity.
This is correct mathematically, and we want you to verify it in Exercise CD-7.5.2.
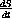 , where S=S[V[t]]. (See review Exercise CD-28.3.2 to express surface area as an explicit function of volume.)
, where S=S[V[t]]. (See review Exercise CD-28.3.2 to express surface area as an explicit function of volume.)
Solve the equation x2+y2=L2 for
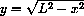 . Use the fact that x=x[t] is a function of time together with the Chain Rule to show that
. Use the fact that x=x[t] is a function of time together with the Chain Rule to show that
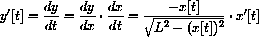
Verify that this model predicts that as x approaches L, the speed of the tip resting on the wall tends to infinity.
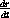 , the rate of change of radius with respect to time?
, the rate of change of radius with respect to time?
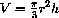 .)
.)
7.6.1
7.6.2