8.2
In the Mathematical Background on CD, we prove a general existence and uniqueness result for continuous dynamical systems.
The proof includes showing that Euler's approximation converges as the step size
Simply put, the theorem means that saying y[t]=Y0ekt is exactly the same thing as saying y[0]=Y0 and
Let
Now consider the function
This is the same dynamical system, written with a different letter.
Uniqueness means that both y[t] and z[t] are the same function
Our new definition causes us a technical problem.
We know how to compute rational powers of e. We want to show that the new definition extends what we already know.
Problem CD-8.1
8.5
8.1.1
8.3
8.4 Section Summary
The important functional identity exey=ex+y follows from the differential equation defining the exponential function.
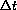 tends to zero.
Mathematical uniqueness of the solution to an initial value problem is what makes dynamical systems deterministic scientific models.
Uniqueness is really what you are thinking of when you say, "The solution of this system models ...." Uniqueness is also mathematically important.
For now, we will use the following result:
tends to zero.
Mathematical uniqueness of the solution to an initial value problem is what makes dynamical systems deterministic scientific models.
Uniqueness is really what you are thinking of when you say, "The solution of this system models ...." Uniqueness is also mathematically important.
For now, we will use the following result:
Theorem CD-8.1
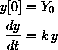
This function can be written y[t]=Y0ekt. 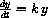 . The theorem assures us in particular that a function
. The theorem assures us in particular that a function
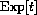 of our official definition exists.
We know intuitively from our experience with programs like SecondSIR and EulerApprox that the computer approximations do converge.
The next subsection shows how the important addition formula for exponentials follows from uniqueness of the solution to our official definition.
of our official definition exists.
We know intuitively from our experience with programs like SecondSIR and EulerApprox that the computer approximations do converge.
The next subsection shows how the important addition formula for exponentials follows from uniqueness of the solution to our official definition.
8.4.1
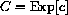 , and consider the function
, and consider the function
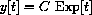 . We know y[0]=C and by the Superposition Rule for differentiation that
. We know y[0]=C and by the Superposition Rule for differentiation that
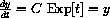 . This means that y is a solution to
. This means that y is a solution to
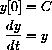
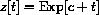 . Again,
. Again,
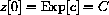 and the Chain Rule says
and the Chain Rule says
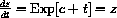 , so z is also a solution to
, so z is also a solution to

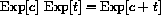
and proves the functional identity of the natural exponential function.
Let e be the number Exp[1], that is, the value of the solution of the dynamical system at time 1.
 .
.
8.5.1
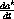
8.5.2