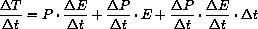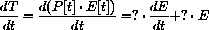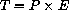 . These are all functions of time, P=P[t], E=E[t], and T=T[t].
. These are all functions of time, P=P[t], E=E[t], and T=T[t].
This project is a small project or big exercise that illustrates the idea of the product rule for differentiation.
The population of a certain country is 15,000,000 people and increasing at the rate of 10,000 people per year. In this country the per capita expenditure for energy is $1,000 per year and is growing at the rate of $8 per year. ("Per capita" means each person spends $1,000 each year.) This project asks you to explore the connection between the country's growth in total yearly energy expenditure and the symbolic product rule.
First do some arithmetic to get a feel for the problem. What will the population of the country be next year? How many dollars will each person spend on energy next year? What will the total energy cost be next year? How much has the total energy cost changed from the first to the second year? What are these same quantities the following year?
Now choose appropriate variables and carefully express the conditions of the problem in terms of your variables and their changes.
For example, let P equal the population at time t (in years) and let E equal the per capita expenditure at time t. The total energy expenditure then is
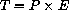 . These are all functions of time, P=P[t], E=E[t], and T=T[t].
. These are all functions of time, P=P[t], E=E[t], and T=T[t].
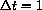 , denote the change in population by
, denote the change in population by
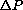 . Denote the change in per capita energy expenditure for a single year by
. Denote the change in per capita energy expenditure for a single year by
 . What is the change in total energy expenditure,
. What is the change in total energy expenditure,
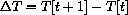 , written as a formula in terms of P, E, and the differences
, written as a formula in terms of P, E, and the differences
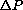 and
and
 ? Illustrate your formulas with numerical examples.
? Illustrate your formulas with numerical examples.
The symbolic question is more difficult, so here are some hints: The change in total energy expenditure for the people P[t] during the next year is
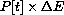 , the difference in their total expenditure in year t,
, the difference in their total expenditure in year t, 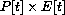 , and the next year,
, and the next year,
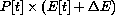 ,
,
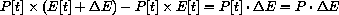
However, this is not all of the new energy expenditure, because there are also new people,
 . These people spend last year's amount on energy,
. These people spend last year's amount on energy,
 , and they also spend the increase in per capita energy,
, and they also spend the increase in per capita energy,
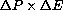 . What is the formula for the one year change in total energy expenditure in terms of P,
. What is the formula for the one year change in total energy expenditure in terms of P, 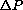 , E, and
, E, and
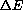 ?
?
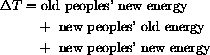
 ?
?
Now we want you to modify your formula for the energy change
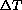 if the time change
if the time change
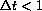 , say
, say
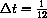 , one month.
The number of new people in one month is the annual rate times
, one month.
The number of new people in one month is the annual rate times
 and in
and in
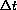 years is the annual rate times
years is the annual rate times
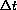 . Let
. Let
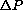 now denote the change in population during the
now denote the change in population during the
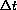 time period.
Since the rate of change of population is assumed constant, we could express this as
time period.
Since the rate of change of population is assumed constant, we could express this as
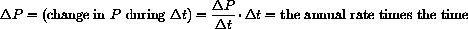
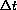 is
is
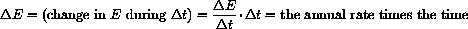
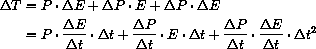
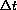 ,
,