Project 5: Max-Min in S-I-R Epidemics
Previous project Next project

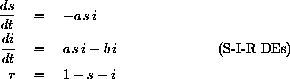
We never found explicit formulas for the functions s[t] and i[t] of the epidemic model of Chapter 2, and this project shows how you can find max-min information anyway.

The epidemic model of Chapter 2 is given by the system of differential equations


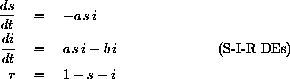
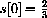and the values of the fractions of susceptible, infective, and removed individuals at the start of the epidemic. For example, we studied the case and . Typically, the initial i[0] is small and s[0] is large but not 1 unless no one has ever had the disease.

  • Begin your project write-up with a description in your own words of how we derive the S-I-R differential equations. (See Chapter 2 of the text.)

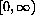  • Prove that the function s[t] is a decreasing function on . What calculus criterion is needed?

    There are two `peaks' of interest in an epidemic. 1) When are the most people sick? 2) When is the disease spreading fastest? The second peak could mean either that the rate of contracting new cases is largest or that the growth in the infectious population is largest. These are different.

    Before you begin, review the mathematical ideas needed to find the maximum of a function defined on the interval 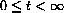. You need to apply the theory to three functions, i[t], f[t]=as[t]i[t], and .

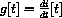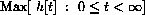
  • Suppose h[t] is a differentiable function. We find

    by .

    For example, the function i[t] has a "typical" slope table, "up"-"over"-"down."


    so

    Moreover,

    and

    Note that s[t] is decreasing, so if s[0]>1/c and later s[tp]=1/c, afterward we must have s[t]<1/c for t>tp.

  • The First Peak of an S-I-R Epidemic
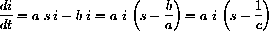
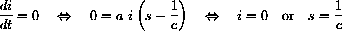
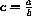    When is the epidemic expanding in the sense that the number of sick people is increasing? If you are thinking in terms of absences from class, when does the epidemic "peak"? Write your condition using a derivative and then express your answer in terms of s and the contact number . Show that the variable increases before your condition and decreases afterward.

    Consider various cases of c and initial conditions in s and i including "extreme" cases such as c very big and very small or s[0] very big or very small. (Note: c=15 for measles and c=4.6 for polio. Nearly everyone is susceptible if s[0]=0.9.) When s[0]<1/c, when does the i[t] "peak"?

  • The Second Peak of an S-I-R Epidemic
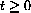    When is the disease spreading fastest in terms of the growth of new cases? What does asi measure? If we want to maximize the function f[t]=as[t]i[t] for , we need to find zeros of its derivative

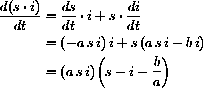
    Show that this is zero when s-i=1/c. When is f[t] increasing? When is f[t] decreasing? What is the slope table of its graph?

    The previous peak does not take the daily recovery rate into account.

  • The Third Peak of an S-I-R Epidemic
    When is the disease spreading fastest in terms of the growth of infectives? In other words, maximize the function . Show that the derivative of g[t] is: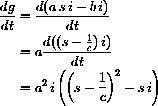

    This equation is hard to analyze, but we can use the invariant from Chapter 2,


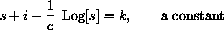
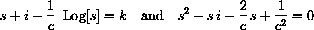
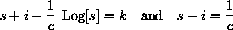
    with the computer to find the crossing points of the curves

    or crossing points of the curves

    Discuss various cases of the value of c and the initial values of s and i.


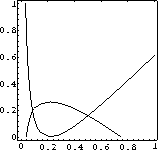
    Figure 5.1: Intersection of the Critical Equation and Invariant

    We can also modify the SIRsolver program to plot the expressions for f'[t] and g'[t] in various special cases.


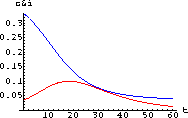
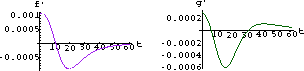
    Figure 5.2: Susceptible and Infectious Fractions


    Figure 5.3: Derivatives of f[t] and g[t] from SIRsolver values of s[t] and i[t]

    These graphs should help you make slope tables for f[t] and g[t] at least in these special cases. (Look at the signs of f'[t] and g'[t] on the graphs.) Of course, you could also graph f[t] and g[t] themsleves.

    Problem 5.1

    Use the program SIRsolver or SIRmaxHelp from our website to examine the three "peaks" of various epidemics. When do they occur? How do the disease parameters b and c affect the peaks and times of occurrence? How do the initial values of s[0] affect the peaks and times?

    Previous project Next project Close this window