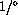 C:
C: We want to investigate the question: How much does the volume of a typical house increase over the course of a normal day's warming? This problem illustrates a number of basic ideas which are generalized in symbolic differentiation formulas, and the numerical answer may surprise you, besides. Do you think it increases by a thimble, a bucket, or a bathtub?
Most solids expand when they are heated in familiar temperature ranges. (Ice near freezing is a notable exception.) Scientific tables list "coefficients of expansion" in units of 1/(units of temperature). Here are a few in units of
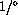 C:
C:

The first question is: What does the "coefficient of expansion" mean? The units are actually (units of length expansion) per (units of length to start) per (units of temperature). The length units cancel.
If the coefficient of expansion is c, the object is initially l units long, and the temperature increases
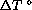 C, then the change in length
C, then the change in length
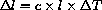
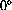 C) warmed to
C) warmed to
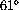 F (=
F (= 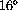 C) increases its length by
C) increases its length by
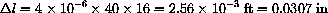
Let's say the interior of the house is a rectangular solid 40 feet long, 30 feet wide, and 8 feet high.
The changes in width and height are

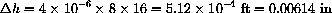
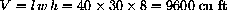
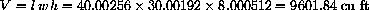
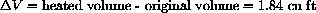

How much does a gold palace the same size as your house expand its volume?
These numbers are interesting in that small linear expansions still produce a fairly big volume expansion, but all the arithmetic is not very revealing in terms of showing us the rates of expansion.
A symbolic formulation can do this for us.
We begin by specifying our variables:

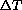 . The coefficient of expansion formula
. The coefficient of expansion formula
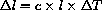 gives us the formulas
gives us the formulas
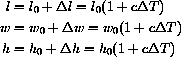
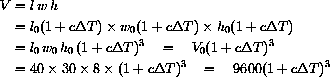
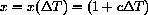
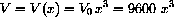
 is
is

 produces the ratio or rate of change
produces the ratio or rate of change
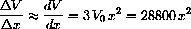
 symbolically.
symbolically.
Now use the definition of the variable x.
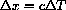 as temperature changes from 0 to
as temperature changes from 0 to
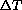 , so
, so
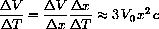
Finally, consider the size of x2 compared with the other terms.
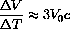
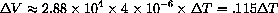
We wanted
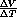 and approximated it in two steps,
and approximated it in two steps,
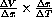 . The chain rule says in general that
. The chain rule says in general that
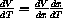 when V is "chained" together from two other functions.
when V is "chained" together from two other functions.
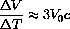
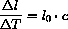
Now give a "practical" application of your formula.
7.1
Once you are comfortable with the symbolic rules of calculus, the large change in volume is easily understood.
The instantaneous rate of thermal expansion of the length x of an object is the derivative
The insight into the large volume expansion is clearest in the initial symbolic formula for expansion
Problem 7.1
The first differential equation describes a straight line of constant slope x0c, so the solution is x=x0(1+cT). We will see in Chapter 8 of the core text that the solution to the second equation is x=x0ecT. Use Mathematicato plot both functions over the range
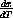 . An object originally of unit length therefore has
. An object originally of unit length therefore has
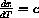 . Our house has dimensions l=40x, w=30x, and h=8x where the initial length x0=1 foot.
In terms of x, the volume of the house is
. Our house has dimensions l=40x, w=30x, and h=8x where the initial length x0=1 foot.
In terms of x, the volume of the house is
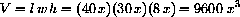
The chain rule says
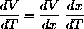
and basic rules give
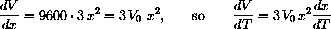
At the initial temperature x=1, thus we have
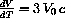 or, in terms of differentials, the change in V is given by
or, in terms of differentials, the change in V is given by
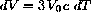
Numerically, 3V0c=.115, so that a change of temperature of dT=16 produces an approximate change in volume of
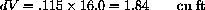
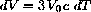
because the triple volume compensates for the small linear expansion coefficient, c.
While the linear expansion is small on our familiar scale, the volume seems larger - a bathtub full.
However, it might be more reasonable to compare the change in volume to the amount we started with.
Write an expression for the percentage change in volume and solve for that in terms of c and the change in temperature.
Show that the percent change in volume is three times the percent change in length.
Do the scientific tables giving thermal expansion per unit length mean that
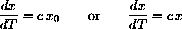
where x0 is the fixed length at the initial temperature, while x is the varying length as temperature changes?
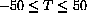 with x0=1 and
with x0=1 and
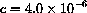 . What do you observe? In particular, what is the largest difference between (1+cT) and ecT over this range?
. What do you observe? In particular, what is the largest difference between (1+cT) and ecT over this range? 