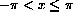Project 51: Computation of Fourier Series
Previous project Next project

Fourier series and general "orthogonal function expansions" are important in the study of heat flow and wave propagation as well as in pure mathematics. The reason that these series are important is that sines and cosines satisfy the "heat equation" or "wave equation" or "Laplace's equation" for certain geometries of the domain. A general solution of these partial differential equations can sometimes be approximated by a series of the simple solutions by using superposition. (Fourier series provide many interesting examples of delicately converging series because of Dirichlet's theorem 13.4 of the Mathematical Background.)

The method of computing Fourier series is quite different from the methods of computing power series. The Fourier sine-cosine series associated with f[x] for 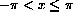is:


where

and for k=1,2,3,...

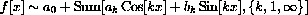
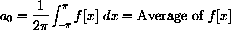
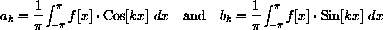
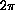Dirichlet's theorem says that if f[x] and f'[x] are -periodic and continuous except for a finite number of jumps or kinks and if the value f[xj] is the midpoint of the jump if there is one at xj, then the Fourier series converges to the function at each point. It may not converge uniformly, in fact, the approximating graphs may not converge to the graph of the function, as in Gibbs' goalposts below. If the periodic function f[x] has no jumps (but may have a finite number of kinks, or jumps in f'[x]), then the series converges uniformly to f[x].

Convergence of Fourier series is typically weaker than the convergence of power series, as we shall see in the examples, but the weak convergence is still quite useful. Actually, the most important kind of convergence for Fourier series is "mean square convergence,"


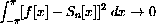
where Sn[x] is the sum of n terms. This is only a kind of average convergence, since the integral is still small if the difference is big only on a small set of x's. We won't go into mean square convergence except to mention that it sometimes corresponds to the difference in energy between the "wave" f[x] and its approximation Sn[x]. Mean square convergence has important connections to "Hilbert spaces."

Convergence of Fourier series at "almost every" point was a notorious problem in mathematics, with many famous mathematicians making errors about the convergence. Fourier's work was in the early 1800s and not until 1966 did L. Carleson prove that the Fourier series of any continuous function f[x] converges to the function at almost every point. (Dirichlet's theorem uses continuity of f'[x]. Mean square convergence is much easier to work with and was well understood much earlier.)

Three basic examples of Fourier sine-cosine series are animated in the computer program FourierSeries. These are the following.




Figure 51.1: Fourier Series for f[x]=|x|

The average value of f[x] is clearly 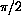and can be computed as the integral


Notice the step in the computation of the integral where we get rid of the absolute value. We must do this in order to apply the Fundamental Theorem of Integral Calculus. Absolute value does not have an antiderivative. We do the same thing in the computation of the other coefficients.



using integration by parts with

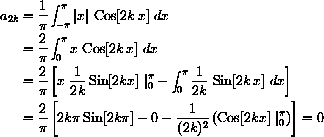
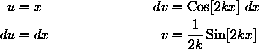
  • Show that the ak terms of the Fourier series for f[x]=|x| with odd k are


    and all bk=0.


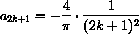
    Without the absolute value the integrals of the Fourier coefficients can be computed directly, without breaking them into pieces.


    Figure 51.2: Fourier Series for f[x]=x

  • Calculate the coefficients of the Fourier sine-cosine series for f[x]=x, for , extended to be 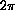periodic. Notice that the average a0=0, by inspection of the graph or by computation of an integral. Moreover, 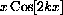is an odd function, that is, 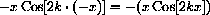, so the up areas and down areas of the integral cancel, ak=0. You can compute this from the formula. Finally, show that


    The coefficients for the Fourier series of


    must be computed by breaking the integrals into pieces where the Fundamental Theorem applies, for example,

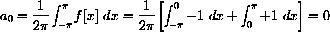
  • Show that


    and

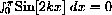    because each piece of the integral , being the integral over whole periods of the sine function.

    Finally, show




    Figure 51.3: Gibbs Goalposts

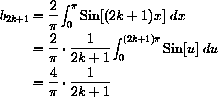
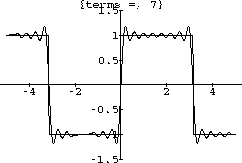
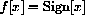
    The convergence of the Fourier series for Sign[x] holds at every fixed point, but the convergence is not uniform. In fact, the graphs of the approximations do not converge to a "square wave," but rather to "goalposts." Each approximating term has an overshoot before the jump in Sign[x] and these move to a straight line segment longer than the distance between . You can see this for yourself in the animation of the computer program FourierSeries.

    Previous project Next project Close this window