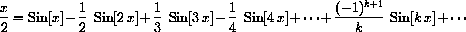
Project 50: Rearrangement of Conditionally Convergent Series
Previous project Next project

Dirichlet's theorem 13.4 from the Mathematical Background book (on the CD) gives us the convergent expression


but notice that the simple absolute value estimate of Weierstrass' majorization from Section 25.2 of the main text leads to no conclusion when we estimate

since the harmonic series diverges,

Dirichlet's theorem for Fourier series is very powerful, because it gives us results where great care is needed for direct convergence proofs. (The proof of Dirichlet's theorem uses integration by parts somewhat like the proof of Taylor's formula.)

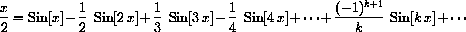
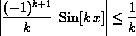
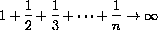
We emphasized absolute uniform convergence in the main text, because that kind of convergence allows us to treat series the most like very long sums. This section shows you an example of the strange nature of series that do not converge absolutely. Actually, we could expand on the specific idea and show that for any number r or 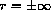, we can rearrange the terms of a conditionally convergent series so that it sums to r. By rearranging terms, we can get any sum we choose! (The proof of this is not very hard, but it is more abstract than the specific example we give.)

We showed in Example 27.1 of the main text that


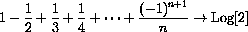
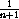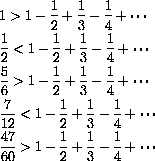
converges and that it even has an error no more than , since the approximating sums alternate up and down with decreasing size oscillations. However, we want you to observe that rearranging these same terms results in a different limit, specifically, PROVE THAT:

  • Show that the rearranged alternating harmonic series above may be written symbolically as

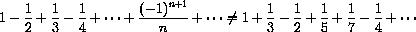
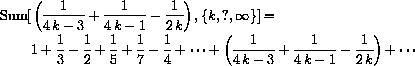
  • Prove that 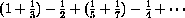the grouped terms produce decreasing oscillations, that is,

  • Also prove that each of the terms grouped as in the first expression is positive,

    and use this to prove that the rearranged series converges and

  • Clearly, the terms of the alternating series

    sum with decreasing oscillations, so prove that

  • Combine your results to show

    (Note: .)

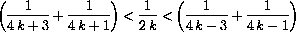
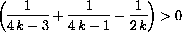
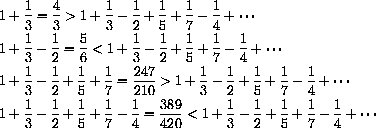
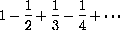
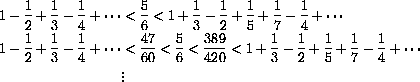
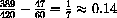    You are welcome to use the symbolic summation of the computer. For example, to compare these series with Mathematica, you could type the program:

    T := Sum[(1/(4 k - 3) + 1/(4 k - 1) - 1/(2 k) ,{k , 1, n}] ;

    S := Sum[1/(2 j - 1) - 1/(2 j) , { j , 1, n}] ;

    Do[

    Print["T = " , T , "S = " , S , "n = " , n, "Diff approx =", N[T - S]]

    ,{ n , 1, 10 } ]     <Enter>

    Previous project Next project Close this window