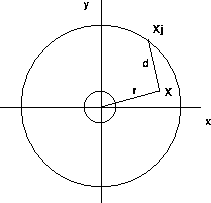
Figure 47.1: Solar System in Two Dimensions
In order to provide a spacecraft with sufficient energy to escape the solar system, Jupiter can be used to "boost" its orbit. We want to determine the necessary relationship between the spacecraft's original trajectory and Jupiter's orbit, so that Jupiter will boost the spacecraft out of the solar system. This requires that they pass close enough for Jupiter to exert a definite effect, while not close enough for Jupiter to "catch" the spacecraft. To determine the relationship, we must find the general equations of motion.
We take the origin of the coordinate system at the sun. In order to simplify matters, the solar system is represented in two dimensions, with the coordinate axes in the plane of the orbits of the planets. Figure 47.1 is a diagram of the system. In the diagram, the vector X points from the sun to the spacecraft and the vector XJ points from the sun to Jupiter (the inner circle represents the earth's orbit, while the outer circle represent Jupiter's orbit).


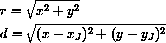
Kepler's third law states that the square of the period of a planet is proportional to the cube of its mean distance to the sun, specifically,
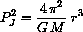
The period and frequency of Jupiter's orbit about the sun are given in these units by
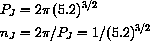
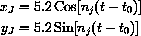
When t=0, where is Jupiter?
How long does it take for Jupiter to complete one revolution about the sun?
47.2
Newton's law of gravity says that an object of mass m and a second object of mass M attract each other with a force of magnitude
47.3
Newton's "F = m a" law can now be applied to find the equations of motion of the spacecraft:
In order to use this system of equations, we need to interpret our original equations as a corresponding set of four first-order differential equations, which can then be evaluated and plotted as functions of time using the JupiterHelp program.
You learned the "phase variable trick" in Chapter 23 of the core text, and so the derivation is left to you.
47.4
Use the JupiterHelp program to find initial conditions that will "sling" your spacecraft out of the solar system.
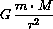
where r is the distance between the objects.
The force acts along a line connecting the centers of the objects.
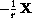 is a unit length vector pointing from the spacecraft toward the sun.
is a unit length vector pointing from the spacecraft toward the sun.
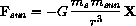
 is a unit length vector.
In what direction does it point?
is a unit length vector.
In what direction does it point?
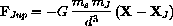
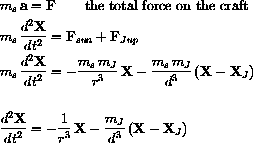
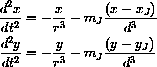
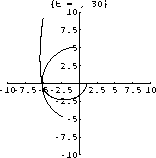
Figure 47.2: Escape from the Solar System