
Figure 45.1: A Hypothetical Bomb Trajectory
This project models low-level bombing with differential equations. This involves determining where a bomb lands when you drop it from a specific height and velocity, or when and where to release a bomb when you are given a specific, stationary target. The two ideas are Galileo's law of gravity and air friction due to the high speed of the bomb. They are combined with Newton's law, F=mA. Vectors play a role, because the air friction is an increasing function of speed, not velocity.

We place a coordinate system with its origin at the target with the horizontal x-axis aligned so the plane has positive x-vleocity. We will use mks units, so the gravitational constant g=9.8.
ESSENTIAL VARIABLES

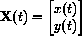 is the position vector of the bomb, V =
is the position vector of the bomb, V =  is the velocity vector, and its length is the speed of the bomb.
Acceleration is the vector
is the velocity vector, and its length is the speed of the bomb.
Acceleration is the vector
 .
.
We will model air friction by assuming that the force due to air friction is proportional to a power of the speed and acts in the direction opposite the velocity vector, |Fair|=ksp, with the same direction as -V.
PARAMETERS
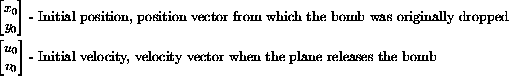

One of the two forces acting on the bomb as it falls is air resistance, Fair. This force acts to slow the bomb opposite to the direction in which the bomb tries to travel. It acts in an opposite direction to the velocity vector at any given time, as Figure 45.2 illustrates.
2) What is the unit vector in the direction opposite V, or in the direction of Fair?
3) Using the results from the two previous exercises, show that

The other force acting on the bomb is due to the weight of the bomb due to gravity. The force due to gravity varies according to mass and has magnitude mg, where g is the acceleration due to gravity, approximately equal to 9.8 meters/second2.
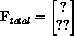
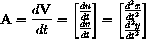
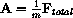 ,
, 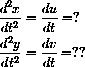
In order to use the AccDEsoln program to solve the equations, you must use the phase variable trick. This transforms the two second-order differential equations that you just derived into a system of four first-order differential equations.
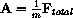 in terms of first derivatives and the phase variables.
in terms of first derivatives and the phase variables.
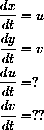
These four equations can be plugged into the AccDEsol program; however you also need the initial conditions.
A plane flying horizontally at height h, a horizontal distance j before the target at speed si gives:

 in a vertical drop, we have the equations
in a vertical drop, we have the equations
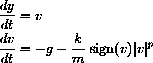
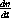 ? Solve this equation for k in terms of p and compute the specific values for p=1,7/5,2.
? Solve this equation for k in terms of p and compute the specific values for p=1,7/5,2.
45.1
The vector nature of the air resistance means that a bomb released at high speed will have a big vector force opposite to its direction of motion.
If the bomb is inclined downward, the resistance will therefore have an upward component.
The bomb won't fall if this component of resistance equals its weight.
Of course, the resistance slows the bomb down horizontally, so it does not fly along with the bomber for long.
Once it slows down, weight exceeds the upward component of resistance and it falls faster and faster until the vertical resistance again builds up.
Problem 45.1
Low-Flying Bombs
Now that you have a good understanding of how this model works and what the equations mean both graphically and mathematically, it is time to put the computer to work.
Problem 45.2
Hitting the Target
It is also interesting to follow the path of the bomb.
This can be graphed with the computer's help.
In addition, you can follow the descent by following the angle the tangent line to the bomb's path forms with the ground.
This can tell you the angle at which the bomb hits, or if the bomb nearly "floats" when first released.
Problem 45.3
Run some computer experiments with bombers flying 350 mph (be careful with units), dropping bombs from various initial heights.
Use several values of the resistance power p and its associated k. Show that the flying effect of bombs is most important in hitting a target if you wish to bomb from a low level.
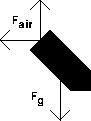
Figure 45.3: Force Components
You are flying at altitude h at velocity si and decide to drop a bomb.
Where do you release the bomb so that it hits the target at (0,0)? Use several values of p. How much room for error do you have in releasing the bomb so that you will still hit within a meter of your target? How does varying your altitude and initial velocity affect the room for error that you have?
Determine the angle at impact of the bomb.
How do changes in h and si affect this?