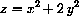
This project investigates the 3-D effect of sliding down a slippery slope. The component of the force due to graivty acts opposite the gradient, but motion under this acceleration does not produce gradient trajectories. You don't just ooze to the bottom, but zoom right on by. Problem 18.2 of the core text found the gradient trajectories. Exercise 17.7.6 found the tangential component of a force acting on a plane. We begin with a quick reminder about those problems.
Perfecto Ski Bowl has the shape of the surface
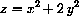

A skier falls somewhere on the slope above (x0,y0) with initial velocity zero but is without control of direction; his edges are in the air.
The skier's weight vector is


Newton's "F = m a" law says that the mass times the acceleration of the skier,
 , equals the total force on the skier,
, equals the total force on the skier,
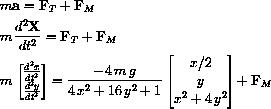
44.1
A skier at rest will only have the tangential component of gravity acting on him, but in motion, the mountain must contribute a force.
We want you to see a simple case of this force without worrying about gravity.
The vector function
Suppose that we want the speed of the motion to be s. Show that we need to take
It is easiest to represent our mountain implicitly
The force due to the mountain will be a scalar multiple of the perpendicular vector,
We want to compute
The equation above can be written in components as
44.2
We use this fact about any motion on h[X[t]]=j together with the fact that the tangential force is perpendicular to
Test your formula on the case of constant speed s motion around the circle x2+y2=r2, z=0. Newton's law with no tangential force becomes
44.3
We may view the pendulum (described in Project 46) as a motion on a circle
44.4
Suppose that the surface constraining the motion can be expressed as an explicit function of x and y,
Notice that the z variable does not appear in the equations for x, y, u, and v. This means that we could solve the pair of second-order equations for x and y, or
Now put it all together:
Problem 44.1
Use the phase variable trick from Chapter 23 of the core text to write the equations of motion for the skier as a differential equation:
Use the PerfectoHelp program from our website to solve these equations for several choices of the initial conditions.
Does the skier stop at the bottom?
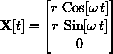
moves at constant speed around the circle of radius r, given implicitly by x2+y2=r2 and z=0.
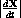 and
and
 and show that they are all different constants.
and show that they are all different constants.
 , so
, so
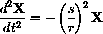
The acceleration of a circular "mountain" on a "skier" at constant speed s is s2/r in the direction
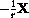 .
.

For example, for Perfecto, we can take the function h[x,y,z]=x2+2y2-z and the implicit equation, h[x,y,z]=0. The reason we want to use this form is so we have a simple way to find a normal to the mountain.
In this case, the gradient
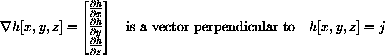
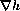 is perpendicular to Perfecto Ski Bowl when h=x2+2y2-z.
is perpendicular to Perfecto Ski Bowl when h=x2+2y2-z.

Test your formula in the case F=(0,0,-mg) and h[x,y,z]=x2+2y2-z.
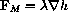 , and
, and
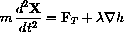
 , knowing that it somehow depends on the curvature of the mountain and the skier's speed.
, knowing that it somehow depends on the curvature of the mountain and the skier's speed.

Differentiate this equation once with respect to t and show that
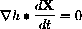
What does this equation say about the direction of the velocity of the motion X[t]?

If we differentiate this equation with respect to t again using the Product Rule and Chain Rule, we obtain
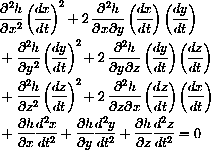
Notice that the last line of this derivative contains the dot product
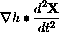
We summarize the computation in matrix notation

where h(2)[X] is the matrix of second partial derivatives of the constraint function h[X]. Notice that this term involves the velocity and second partials related to the curves on the mountain.
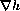 to derive a formula for the scalar
to derive a formula for the scalar
 :
: 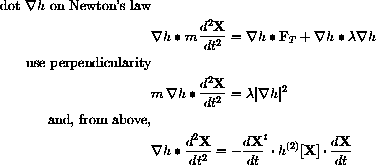
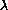 :
: 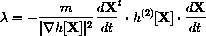
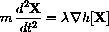
Now compute the specific quantities: 

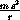 in the direction
in the direction
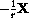 . Simplify the expressions in this special case and show that the formula
. Simplify the expressions in this special case and show that the formula
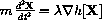 agrees with this,
agrees with this,
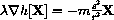 .
.

so h[x,y,z]=x2+y2. The only applied force is still gravity which we take as F=(0,-mg,0).

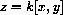
The constraint h[x,y,z]=j can be written h[x,y,z]=k[x,y]-z=0 for the general formulas.

and compute this quantity for the Perfecto Ski Bowl function.
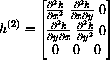
and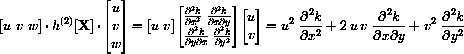
and compute this quantity for the Perfecto Ski Bowl function.

and compute this quantity for the Perfecto Ski Bowl function.
 ,
, 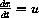 ,
, 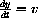 ,
, 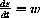 , and
, and
 . Show that the equations of motion on z=k[x,y] may be written
. Show that the equations of motion on z=k[x,y] may be written

and write these equations for the Perfecto Ski Bowl function.
 ,
, 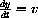 , and
, and
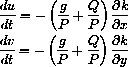
together with initial conditions and find functions x[t] and y[t]. We could then simply let z[t]=h[x[t],y[t]].
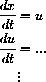
In a program, you can "fill in the blanks" in simple steps using computer derivatives and the formulas above.
Solve your equations and plot the path of the skier.