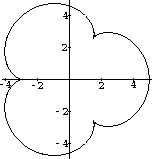
Figure 43.1: An epicycloid
A small wheel rolls around a large fixed wheel without slipping. What path does a point on the edge of the small wheel trace out as it goes? You can answer this quaestion with vectors and an understanding of radian measure. The Spirograph toy makes such plots, called "cycloids." Figure 43.1 is a sample path.
This is not trivial. Vectors help, and here is a special case to show you why. Suppose the large wheel has radius 3 and the small wheel has radius 1. How many turns must the small wheel make while traveling once around the large wheel? This is a famous question because it appeared on a national college entrance test as a multiple-choice question. The reason it is famous is that the correct answer was not among the choices.
Here is the obvious solution: The big wheel has three times the circumference of the small wheel (you can use
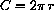 ), so the small one must mark off three revolutions to cover the same distance and travel all the way around the large one.
Obvious, but wrong.
The small wheel turns four times.
Run the computer animation in EpiCyAnimate to see for yourself (Figure 43.2).
), so the small one must mark off three revolutions to cover the same distance and travel all the way around the large one.
Obvious, but wrong.
The small wheel turns four times.
Run the computer animation in EpiCyAnimate to see for yourself (Figure 43.2).
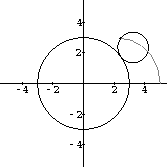
43.1
We will use vectors to analyze the motion of a point on the little wheel.
This will give us parametric equations for the whole path but also show us why the small wheel turns four times in the 3-to-1 ratio case.
You will need to know that the length of a circular segment of angle
We begin with one vector
We also have a second vector,
The vector
After a small increase in
The length of portion along the big wheel where contact has been made is
43.2
The vector pointing from the center of the wheel to a reference point on the wheel has the form
The distance moved along the line at time t is
43.3
Problem 43.1
The Hypocycloid
If the large wheel has radius 3 and the small wheel has radius 1, how many turns does the small wheel make when going around the large wheel once for the epicycloid? For the hypocycloid? (What is
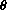 and radius r is
and radius r is
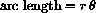
For example, the length all the way around a circle of radius r is what we get when we go an angle
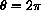 , so
, so
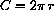 .
.
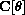 pointing to the center of the small wheel.
We know from the sine-cosine discussion that
pointing to the center of the small wheel.
We know from the sine-cosine discussion that
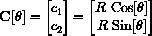
if
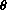 measures the angle from the x-axis and R=rb+rs, the sum of the radii of the large and small wheels.
measures the angle from the x-axis and R=rb+rs, the sum of the radii of the large and small wheels.
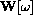 , pointing from the center of the small wheel to the tracing point on its rim.
Again using sine-cosine, we have
, pointing from the center of the small wheel to the tracing point on its rim.
Again using sine-cosine, we have
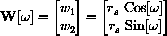
where
 is the angle measured around the small wheel starting from the horizontal and rs is the radius of the small wheel.
is the angle measured around the small wheel starting from the horizontal and rs is the radius of the small wheel.
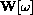 is a displacement; it does not start at the origin.
The position vector interpretation is simply that
is a displacement; it does not start at the origin.
The position vector interpretation is simply that
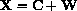
is the arrow from the origin to the reference point on the small wheel.
This may be written in components as
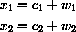
where the components of C and W are given by the formulas above.
The two vectors start in the position shown in figure 43.3 with both pointing to the right of their centers.
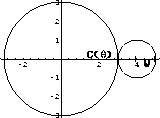
Figure 43.2: Starting Position
 , the vectors look as in Figure 43.4.
, the vectors look as in Figure 43.4. 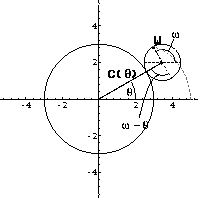
Figure 43.3: Position after Rotation
 . The portion contacted along the small wheel is
. The portion contacted along the small wheel is
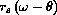 because the contact point lags behind the original horizontal reference line. "No slipping" means that equal lengths are marked off along both wheels, so
because the contact point lags behind the original horizontal reference line. "No slipping" means that equal lengths are marked off along both wheels, so
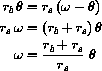
Consider the case where rb=3 and rs=1. When
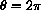 so that the small wheel has gone all the way around the large wheel, we have
so that the small wheel has gone all the way around the large wheel, we have
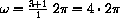 . The small wheel turns four times a full turn.
The computer program Cycloid on our website contains the formulas for the epicycloid we have just derived and uses them to plot the curve.
We want you to extend the idea of using parametric circles and vector addition together in the next exercise.
. The small wheel turns four times a full turn.
The computer program Cycloid on our website contains the formulas for the epicycloid we have just derived and uses them to plot the curve.
We want you to extend the idea of using parametric circles and vector addition together in the next exercise.
A wheel of radius rs=1 rolls to the right along a straight line at speed v without slipping.
The vector pointing to the center of the wheel has the form
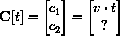
where t is the time.

Figure 43.4: Start of a Cycloid
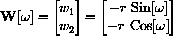
In what position does the wheel begin?
Figure 43.5: After a Small Change
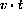 . How much is the distance marked along the wheel in terms of
. How much is the distance marked along the wheel in terms of
 ? Equate these, assuming no slipping, and find
? Equate these, assuming no slipping, and find
 in terms of t. Modify the computer program Cycloid to plot this curve, known as a cycloid.
in terms of t. Modify the computer program Cycloid to plot this curve, known as a cycloid.
A small wheel of radius rs rolls around the inside of a large fixed wheel of radius rb. Use vectors to find parametric equations for the path of a point on the tip of the small wheel and plot the path using the computer.
Three main things change compared with the epicycloid above: First, the small wheel rolls in the opposite direction to its center.
You could account for this by taking
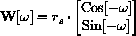
Why does a negative angle correspond to clockwise rotation? Second, the distance from the center of the big wheel to the center of the small wheel is no longer the sum of the radii.
Third, the equation that says the same lengths are contacted along the large and small wheels (or no slipping occurs) is different.
This time the opposite rotation causes angles to add in the length equation along the small wheel.
 when
when
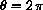 ?)
(Optional) What happens if you use the epicycloid program and equations with r=-1 or a negative rs in general? Try this with computer, and then show that the curve really is a hypocycloid but corresponds to drawing the curve with a Spirograph starting the small wheel in a different position.
?)
(Optional) What happens if you use the epicycloid program and equations with r=-1 or a negative rs in general? Try this with computer, and then show that the curve really is a hypocycloid but corresponds to drawing the curve with a Spirograph starting the small wheel in a different position.