Calculus: Project 41

Project 41: Competition and Cooperation between Species

The concept of an interspecific relationship is not new - in fact, we have been dealing with one such relationship all along - a predator-prey interaction is an interspecific relationship. However, there are other interspecific relationships manifested on the Sogapalag island. While these relationships are fascinating to study as factors contributing to the predator prey interactions, the professor fears that the math involved in such a computation would be entirely over his head. Luckily, he finds several islands with sparrows and rabbits, but no weasels. We will therefore restrict our studies to include only two species. You might, however, try to discuss hypothetical implications of these relationships on rabbits, weasels, and sparrows for islands that have all three species.

41.1 Biological Niches Biologically, we say that two species are competing when the presence of each detracts from the growth of the other. Rabbits and sparrows have partially overlapping niches, that is, they both eat grass and bushes, but the sparrows prefer bushes and the rabbits prefer grass. In general, a niche is defined as the collection of all necessary resources that define a species' way of life. Since the Sogapalag Islands have only grass and bushes, rabbits and sparrows, and weasels, the niches of rabbits and sparrows overlap by the extent to which they cannot choose their separate preferences in food and shelter. According to biologists, no two species may share the same niche, as one will inevitably be a superior competitor, driving the other to extinction or to develop a new niche. However, niches may partially overlap, with one or more common resources.

A mathematical model for competition between species can be formulated as the differential equations:

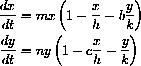
where

VARIABLES:

1. t = time in weeks

2. x = density of hundreds of rabbit pairs per square mile

3. y = density of hundreds of sparrow pairs per square mile

We have already analyzed two cases of this model in Chapter 22 of the text. The first, titled "competition," was written in simplified form, but equivalent to

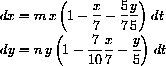
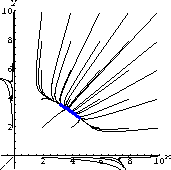
Figure 41.1: Coexistence

The second case of this model was titled "Fierce Competition" and was

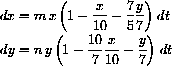
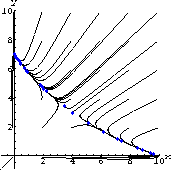
Figure 41.2: Weak Exclusion

We have purposely written the equations with the parameters b and c times the fractions 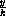and 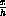. The appetites of rabbits and sparrows are different, corresponding to their different sizes, so we want to measure the effect of a number of sparrows on the rabbits in terms of the carrying capacity of sparrows. For example, without the other species, the environment might support 1000 sparrow couples or 400 rabbit couples per square mile. If there are 500 sparrow couples, half the environment's capacity, 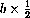tells us the negative affect on rabbits. All things being equal, you might expect "fair" competition to result in half rabbits and half sparrows, but a "fair" meaning to `half and half' should take the various appetites into account. Half and half in terms of carrying capacity would mean 500 sparrow couples and 200 rabbit couples.

The Intensity of Competition
Begin your work on competing species by writing a biological explanation of the model for Professor Debrainman. The parameters h and k are the carrying capacities of an island for each species when the other is absent. Explain this to the professor by reviewing the logistic equation from Chapter 22. The parameters m and n are the intrinsic fertilities of the species, similar to the a parameter in the predator-prey model above. Explain the coefficients b and c carefully to the professor in terms of how effectively one species competes against another. Give the units of each parameter with your explanation. And remember that the explanations are supposed to be as biological as possible, so that we don't terrorize the poor professor.

The parameters b and c are the most difficult to explain. You may want to think of some special cases to help. For example, if bushes are scarce so that both rabbits and sparrows rely mostly on the same resource, grass, then rabbits may heavily affect the sparrow population, who are rendered homeless if their bush is eaten. Sparrows may gobble grass that the bunnies can't then eat, but they will be at a disadvantage. What sorts of choices of b and c describe this situation?

A robust island with plenty of grass and bushes will allow the species to live in separate niches. The sparrows eat only a little grass and the rabbits eat only a few bushes. In this case, the impact of each species on the other is smaller. What are good choices of b and c to describe this situation?

You may want to come back to review your explanation after you have worked more on the mathematical experiments and analysis.

You should review the geometrical analysis of the two competition examples from Chapter 22 of the text. The first example leads to coexistence of rabbits and sparrows, but the second usually leads to the extinction of one or the other, but not both. This is "competitive exclusion," but a weak kind where the surviving species depends on the relative sizes of the two populations at the start of observation.

Mathematical Experiments
Use the computer program Flow2D or the CowSheep example to try some mathematical experiments with various values of the parameters. Begin with m=n=1, h=7, k=10 and then run cases for the following islands.

1. Peaceful Island, b=2/3, c=3/4.
2. Bushy Island, b=3/2, c=3/4.
3. Grassy Island, b=2/3, c=4/3.
4. Anxious Island, b=3/2, c=4/3.

Observations and Conjectures
Summarize your mathematical experiments in the form of some basic conjectures about the two species competition model. What do you think the controlling mathematical factor is in determining the outcome of the competition?
Some of the algebra is simpler if we rewrite the basic equations in terms of new variables,

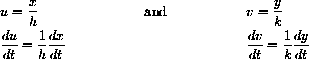
The competition equations become

Proofs:
Prove your conjectures by making the compass heading direction fields similar to those in the text, but strictly in terms of the parameters h, k, b and c. Recall that the direction field is vertical, or dx=0, on the line 1=x/h+by/k. This line crosses the x-axis at h and the y-axis at k/b. The direction field is horizontal, or dy=0 on the line 1=cx/h+y/k. This crosses the y-axis at k and the x-axis at h/c. The relative locations of the pairs of points (h,0) and (h/c,0) and (0,k) and (0,k/b) corresponding to the four cases above can be filled in on the blank graphs in Figure 41.7 to get you started. (If you use the (u,v) dynamics, these points are (1,0) and (1/c,0) and (0,1) and (0,1/b).) Does it matter biologically whether or not the lines intersect in the second or fourth quadrant when c>1 and b<1? Are there other cases?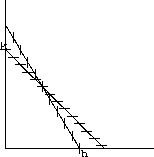

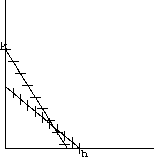
: Four Kinds of Competition between Species

Analytical Proofs QQ.MID.EXER.QQ The computer program LocalStability performs the computations necessary to use the Local Stability Theorem for Continuous Dynamical Systems on these competition equations. This offers an analytical alternative to the simple geometric solution of the problem given in the previous exercise.
41.2 Cooperation between Species There is one small chain of idyllic islands on Sogapalag that are unique. Grass and bushes are present in perfect balance with rabbits and sparrows and they have no weasels. The rabbits fertilize the bushes in the process of eating the excess berries that the sparrows knock off the bushes. The fertilization makes the bushes more fertile and helps the sparrows, while the berries supplement the rabbits' diet. The dynamics are described by the equations: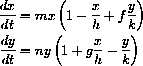

where f and g are coefficients for cooperation. We may also write the equations in terms of the natural un-cooperative carrying capacities by a change of variables,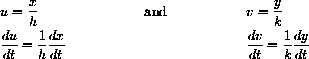

The cooperation equations become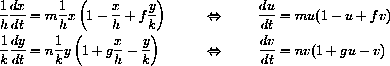

Locate and characterize all nontrivial equilibrium points of the cooperation equations. Show that there is a positive equilibrium at (x_e,y_e) when 1>fg,

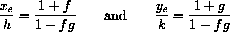
Try some mathematical experiments with various values of the parameters. Try modest cooperation with f=1/4 and g=1/2 and extreme cooperation with f=1.5 and g=1.25

Make compass heading charts like the ones in the text to show that there are two qualitatively different levels of cooperation between the species of this model. Modest cooperation raises both species above the natural uncooperative carrying capacity of both species, while larger amounts of mathematical cooperation lead to a biologically unrealistic case. What is the biological interpretation of both parameters satisfying f>1 and g>1?

: Two Kinds of Cooperation between Species

Previous project Next project Close this window