Resonance is a peak in vibration as you vary the frequency at which you "shake" a system.
For example, many old cars have speeds where they hum loudly, say at 47 mph.
Slower, it's quieter and faster it's also quieter.
We will see this phenomenon in the solution of the linear system
By our study of "transients" in Project 36, we know that the initial conditions do not matter for long-term behavior of the solutions. We are interested only in the amplitude of the steady-state solution.
The values of h and k in the steady-state solution,
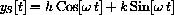
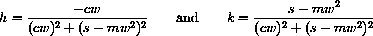
satisfying
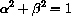there is an angle
, so that
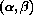. What is its length?)
If we know how to find
so a given
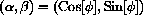, let
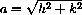, so that
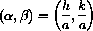
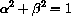and produces an angle
as above.
Use this angle to write
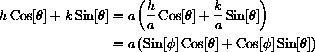
make
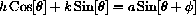
We won't need the converse part, but you can probably see why it holds once you find the formulas for a and
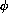in terms of h and k.
37.2
This is called the resonant frequency, and now you should analyze it in various cases of the physical constants.
Use the computer to plot
What happens when
37.3
This is an optional suggestion for an experiment to verify your theoretical calculations.
The series R-L-C electrical experiments work very well, because the components are very nearly linear at low current.
If you can get access to a variable resistor box, a variable capacitor box, an inductor (the bigger the inductance, the better), a wave generator, and an oscilloscope, all of which are in most engineering labs, you can easily build a lab apparatus that illustrates ALL of the things in the above project.
An R-L-C circuit satisfies a linear second-order equation and the wave generator provides the forcing term.
By varying the resistor and capacitor, you can see all the things we have learned - the graphs appear on the oscilloscope! (It is much harder to perform the mechanical oscillator experiments, because it is difficult to vary spring constants and damping friction.)
37.4
The most suspect term in our mechanical oscillator is the damping force
The frequency of oscillation of a linear system
Run the computer program ComplexRoots and observe that initial values that begin on a line in the phase plane remain in line.
Why is this just the geometric representation of the fact that the frequency is independent of the initial condition?
Conduct some computer experiments with the system
How much is
when we write the solution
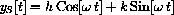
in the form
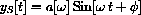
Express your answer in terms of the physical parameters m, c, and s as well as the variable forcing frequency w.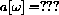 
Simplify the expression for
and show that
is maximized when the square of its reciprocal is minimized.
What frequency
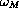minimizes
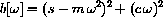
Figure 37.1: 
vs
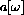versus
for various choices of the parameters m, c, and s. First observe that we have resonance only when 2c2<4ms. Next observe that if 2c2<4ms, then we must have c2-4ms<0. The autonomous system oscillates with "natural frequency"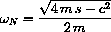 
provided that c2-4ms<0. Explain in your project what this autonomous oscillation means.
Why is this called the "natural frequency?"
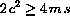, but c2<4ms? What happens if c2>4ms? Verify this mathematical split with some computer plots or experiments.
For damping caused by air resistance, we have investigated nonlinear laws like
(in the bungee project.) The nonlinear 7/5 power makes the damping force grow faster as the speed increases.
This optional section asks how we might detect nonlinearity from the behavior of solutions of the system.
is always the same (provided it oscillates). What is this frequency?
beginning with the ComplexRoots program, by modifying it to solve the nonlinear equation.
With suitable choices of the parameters and suitable scales for your flow, you will be able to see nonlinearity arising as frequencies that depend on the initial conditions.
Explain what you observe.
If the nonlinearity of a shock absorber is small, say
with
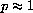, will this be easy to detect in a physical system? What if p is large, say p=3?
so that for all
, 
for all values of
. The max of
is clearly a at the angle where the sine peaks.