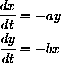
Frederick William Lanchester was an English engineer who died after the end of World War II in 1946. He had a long time interest in aircraft and was one of the first to realize the extent to which the use of air power would alter warfare. The first combat model here was proposed in his 1916 book Aircraft in Warfare published during World War I. His book predicted that "the number of flying machines eventually to be utilized by ...the great military powers will be counted not by hundreds but by thousands ...and the issue of any great battle will be definitely determined by the efficiency of the aeronautical forces." This project investigates some of Lanchester's work on modeling combat.
Two forces numbering x[t] and y[t] are fighting each other.
Lanchester assumed that if the forces were fighting a conventional war then the combat loss rates would be proportional to the total number of enemy forces.
Expressed as a set of differential equations, this becomes
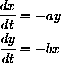


You need to be careful with numerical results for these equations. Negative values of the variables won't make any sense to the model. With this in mind, perform some experiments to get a feel for the behavior of the model.
Experiment with various values of the parameters a and b.
You need to organize the results of your experiments with the explicit time solutions of the equations. Hint 34.3 should give you some ideas about the behavior of the model but at the same time not be easy to summarize. It will be helpful to take another view of the solutions that makes the comparison more natural by plotting both forces on one graph.
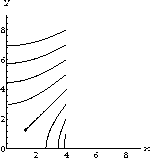
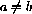 , using the same initial troop strengths as before.
Compare the results obtained by explicit solution with the flow animations.
, using the same initial troop strengths as before.
Compare the results obtained by explicit solution with the flow animations.
A basic kind of comparison is to compute with a fixed-size x force and different initial sizes of the y force. You could make a list of initial conditions, for example, using Mathematica's Table[.] command: initconds = Table[{ 40000,y} , { y,0,80000, 10000} ]
34.1
If one force can concentrate its entire strength on a portion of an opposing army and destroy it, it may then be able to attack the remaining portion of the opposing army with its remaining strength and destroy it.
Lanchester believed air power would be so effective because of this.
An air force can be deployed in full force against select portions of an opposing army.
2) Let the x and y forces have equal effectiveness and let the x-force start at 50,000 and the y-force start at 70,000. Suppose now, however, that the x-force can concentrate its entire strength on 40,000 opposing troops before facing the remaining 30,000 y-force men in a second battle.
How many men are left at the end of the first battle? What is the outcome of the second battle in this instance?
3) Suppose now that an x-force of 50,000 troops is outnumbered by 120,000 y-troops.
Assuming that the x-force can strike a portion of the y-force in full strength and then face the other portion with its remaining men, is there any way for the x-force to win the battle? Justify your answer.
It would be convenient to have a simple analytical method to use to compute answers to questions like those in the exercise above.
Computer simulations can probably give you the answers you need, but there is an easier way
34.2
Consider the case where the two forces have differing combat effectiveness. (In particular, we will use a=0.0106 and b=0.0544 for experiments.
These coefficients have been used to model the course of the battle of Iwo Jima in World War II.) The outcome of the battle in this case is not as clear as with the battles above.
A force of superior numbers may still lose to a smaller force if the combat effectiveness of the smaller force is high.
We can still determine the outcome of a battle, however, by using the differential equations above to derive an integral invariant similar to the energy in a spring or the epidemic invariant or the predator-prey invariant from the CD text Section 24.4. Note that since
The initial values of x and y will determine the value of the arbitrary constant introduced by the integration.
What kind of curves are the integral invariants? For given values of a and b and initial strengths of the x and y forces, how can you use the integral invariant to determine who will win the battle?
Once you have found the invariant formula, you can derive Lanchester's "square law." What is the outcome of the battle if the arbitrary constant you introduced by integrating is 0? What is the outcome if the constant is negative? positive?
34.3
Lanchester's combat equations have been modified to model combat in which one force is a conventional force and one force is a guerrilla force.
The modification takes into account the fact that the fighting effectiveness of a guerrilla force is due to its ability to stay hidden.
Thus, while losses to the conventional force are still proportional to the number of guerrillas, the losses to the guerrilla forces are proportional to both the number of the conventional force and its own numbers.
Large numbers of guerrillas cannot stay hidden and, therefore, derive little advantage from guerrilla combat.
If x is a guerrilla force and y a conventional force, the modified combat equations are:
34.4
In this instance, it is not possible to find an integral invariant as above.
Notice, however, that the expressions describing rates of change are linear in x and y. If this is the case, it can be shown that if e and f are small compared to a and b then the solutions to these equations behave exactly like the solutions to the combat model without operational losses.
You showed above that if the initial conditions are on a certain line through the origin, then the forces mutually annihilate each other.
A unit vector that is drawn in the direction of this line is called a characteristic vector (eigenvektor in German). The key to extending the combat law to this case is in finding an invariant direction or unit vector in the direction.
The computer can find these vectors and enable you to derive a combat law for the model with operational losses.
To do this we first write the differential equation in matrix form.
The computer also has a command Eigenvalues[m] that returns the characteristic roots of the linear dynamical system.
These are the same roots we studied in Chapter 23 of the core text,
In general, if we have an eigenvector-eigenvalue pair for a matrix m,
1) First consider two forces x and y of equal effectiveness.
Suppose the x-force starts with 50,000 men and the y-force with 70,000 men.
Use the rkSoln or the Flow2D program to determine the outcome of the battle if all 50,000 x-troops faced all 70,000 y-troops.
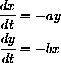
we can take the quotient of
 and
and
 to obtain
to obtain

Now we can separate variables and integrate to get a relationship between x and y. (Review the invariants in CD Section 24.4 of the core text.)
Perform the integration above, remembering that you will introduce an arbitrary constant while integrating.
The solutions x[t] and y[t] will stay on the integral invariant for all time.
Prove this once you have computed the formula as in CD Section 24.4.
Complete the following sentences and derive the square law:
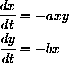
where here again a and b are constants representing the combat effectiveness of each force.
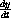 and
and
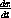 to obtain
to obtain
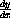 and integrate to obtain an expression involving x and y and an arbitrary constant.
What is the shape of these integral invariants? Derive another combat law:
and integrate to obtain an expression involving x and y and an arbitrary constant.
What is the shape of these integral invariants? Derive another combat law:

Find the integral invariants in this case (they are the simplest of the three models you've seen). What do the invariants represent? Finally, derive another combat law that will enable you to predict the outcome of a battle given certain initial conditions.
Use the Flow2D program to demonstrate your combat law.
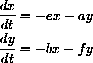
where a and b are the usual combat effectiveness constants and e and f are operational loss rates.
It seems plausible that these should be small in comparison to a and b. This is a linear system like the ones we studied in the text.
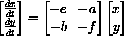
For example, in Mathematicawe can define a matrix in the computer as a list of lists,

The command Eigenvectors[m] will then return two unit vectors.
One will be in the wrong quadrant, but the other will give the direction of the line along which the initial conditions must lie in order for the two forces to mutually annihilate each other.
For example, if a=b=0.1 and e=f=0.001, then the two eigenvectors are given in the list of lists,

The second list is the vector
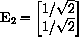
which points along the line "y=x" in the first quadrant.
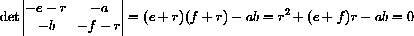
The roots are approximately r1=0.099 and r2=-0.101 in this case.
The single command Eigensystem[m] returns the eigenvalues and eigenvectors.
Eigenvectors and eigenvalues are related by the equation
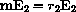
or

In particular,
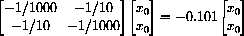
for any constant x0. In this case,

is a solution of the differential equations for any initial vector
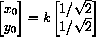
In other words, if x0=y0, then x[t]=y[t]=x0e-0.101t
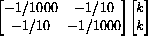
for any constant k. 
holds with r2=-0.101 and
 .
. 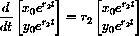
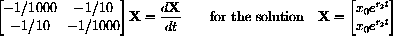

are parametric equations for a ray point toward the origin? In other words, when will the equations trace the line segment starting at (x0,y0) and ending at (0,0) for
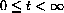 ?
? 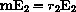
then the vector
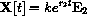
satisfies two conditions: 
and

so that

If the eigenvalue r2 is negative, then the function X[t] is a parametric form of the segment from (x0,y0) to (0,0). In other words, the solution tends to the origin along a line in the direction of E2.