
Figure 33.1: A Smooth Mountain Range
This chapter uses the local stability of a dynamical system to classify critical points as local maxima or minima.

33.1
An ambitious but nearsighted climber on a mountain range of height h,
The statement that "the climber moves in the direction of steepest ascent" can be expressed by the dynamical system
These differential equations stop a path at a critical point (xc,yc) because the critical point condition
33.2
We can use the local stability criteria Theorem 24.6 of the main text to test whether a critical point is a max or min.
This is only a nearsighted local test, because the linearization of the dynamical system is only local.
The linearization of
There are a lot of formulas, so let's review the steps in classifying local extrema.
Let
Classify the critical points of z=3(x2+3y2)e-(x2+y2).

will move in the direction of fastest increase,
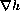 . This is nearsighted in that he may head toward a local maximum or smaller peak, instead of crossing a pass or saddle and climbing the highest peak in the range.
. This is nearsighted in that he may head toward a local maximum or smaller peak, instead of crossing a pass or saddle and climbing the highest peak in the range.

or in components
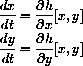
A solution of these differential equations (x[t],y[t]) gives the path of the climber as a function of time by using z[t]=h[x[t],y[t]].
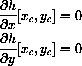
is the same as the equilibrium condition of
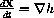 .
.
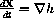 at (xc,yc) is
at (xc,yc) is
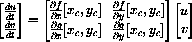
where
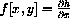 and
and
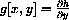 . This makes the linear system matrix
. This makes the linear system matrix

Continuous second partial derivatives are always symmetric,
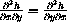 , so the characteristic equation of the linear dynamical system is
, so the characteristic equation of the linear dynamical system is
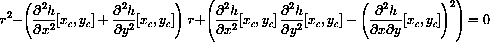
An equation
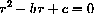
has roots of the same sign if

have the same sign.
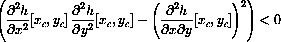
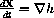 if
if
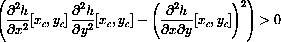
and
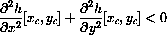
Why is an attractor of the system
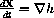 a local maximum for the height function z=h[x,y]?
a local maximum for the height function z=h[x,y]? 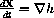 if
if
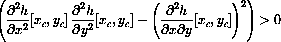
and
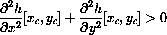
Why is a repellor of the system
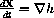 a local minimum for the height function z=h[x,y]?
a local minimum for the height function z=h[x,y]? 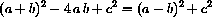
and use it to show that the characteristic equation of this gradient dynamical system cannot have complex roots.
Can you imagine a mountain that spirals you into a max or min by steepest ascent or descent? 
Figure 33.2: 
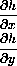
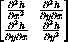
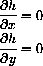
for all critical points, (xc,yc). 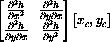
and apply the test in the previous exercise to these numbers.
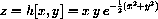 , so
, so
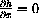 and
and
 at (xc,yc)=(0,0), (1,1), (1,-1), (-1,1), and (-1,-1). Show that the matrix of second partial derivatives is
at (xc,yc)=(0,0), (1,1), (1,-1), (-1,1), and (-1,-1). Show that the matrix of second partial derivatives is
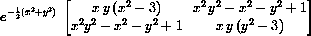
and use the max-min criteria to classify these critical points.

Figure 33.3: z=3(x2+3y2)e-(x2+y2)