The basic idea of least squares fit is this.
We are given data points
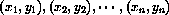
for example, (1,6), (2,9), and (3,10). We know that these represent the output of a linear function
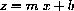
with errors introduced by measurement. We do not know the parameters m and b but wish to estimate them so that they produce the minimal sum of squared errors. What are the squared errors?
Suppose we had chosen a value for m and a value for b. If we compute values using the formula mxi+b and subtract the measured value of yi, we obtain the error at one point,
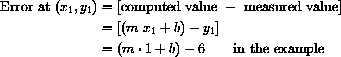
At the input x2=2, we would compute output
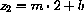 and compare that with y2=9; the difference is
and compare that with y2=9; the difference is
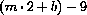 . In this example, the sum of all these actual errors is
. In this example, the sum of all these actual errors is
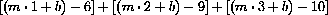
This straight algebraic sum has the disadvantage that a huge positive error and a huge negative error cancel, so that the sum does not represent the "total error." (We do not want two huge canceling errors to be considered small.) The square of an error, like
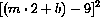 , is always positive and in addition favors small errors,
, is always positive and in addition favors small errors,
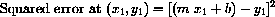
so the sum of the squared errors:
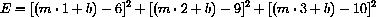
is a measure of overall error that does not cancel errors of opposite sign.
We want to consider the parameters m and b as the unknowns of our problem, so we seek to
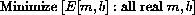
and specifically, we wish to minimize
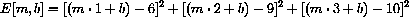
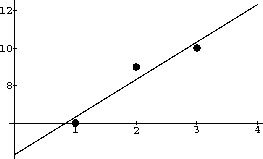
Figure 32.1: Least Squares Fit
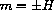 or
or
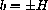 is a huge positive or negative number, then E is huge.
is a huge positive or negative number, then E is huge.
32.2
The exercise above shows that E[m,b] has no maximum.
It does have a minimum, but before we examine the reason, we seek possible locations for the min, that is, critical values or places where the gradient vector is zero.
This is a system of two linear equations in the unknowns m and b,
We have just shown that
The unique solution of these particular linear equations is
32.3
We want you to derive the general formulas for minimizing m and b. Suppose that n pairs of (x,y) values are given,
Notice the n-dimensional norm and dot product in these formulas!
In the example with the data (1,6), (2,9), and (3,10) and least squares fit
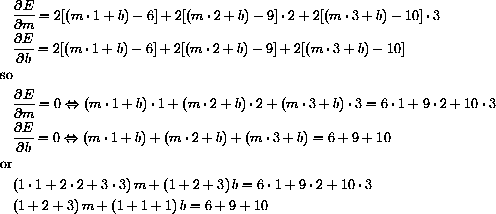
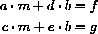
or in the more compact matrix notation
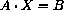 ,
, 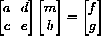
where a=(12+22+32)=14, c=d=(1+2+3)=6, e=3, 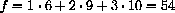 and g=6+9+10=25. The unknowns are m and b.
and g=6+9+10=25. The unknowns are m and b.
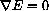 if and only if
if and only if
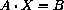 , with the particular matrices,
, with the particular matrices,
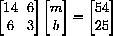
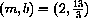 . Verify this by a hand computation.
. Verify this by a hand computation.
Let
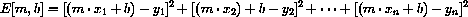
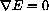 if and only if the unknowns (m,b) satisfy the equations
if and only if the unknowns (m,b) satisfy the equations
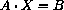 ,
, 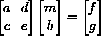
where a=(x12+x22+x32+...+xn2), c=d=(x1+x2+x3+...+xn), e=n, 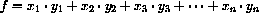 , and g=y1+y2+y3+...+yn
, and g=y1+y2+y3+...+yn
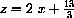 , show that the sum of the signed errors is zero:
, show that the sum of the signed errors is zero: 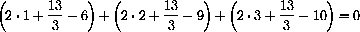
In other words, the amount above and below the fit line is the same.