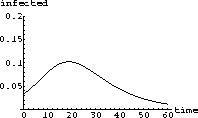
Figure 3.1: Typical Epidemic Infecteds
3.1
Up to this point, all of our disease models have dealt with a disease that spread through the population.
However, there are cases in which the population can attain what is called "herd immunity." In such cases a high enough percentage of the population is immune to ensure that if the disease is introduced to the population, it will simply die out and not spread to form an epidemic.
In order for the disease to die out, the number of infectives must be declining.
The basic question we need to answer is: When will the infectives (i in our mathematical model) decrease?
3.2
Now, consider the case in which the fraction of infectives is zero.
If this is the case, then we can solve for s in terms of r and substitute this into the equation we derived above.
This gives us a relationship between the contact number and the fraction of recovered individuals within the population.
The next exercise is the first big part of your project.
Recall that the first big question is: Why did we eradicate polio, but not measles?
3.3
Do the resulting fractions of immune individuals needed to acquire herd immunity comply with what you might expect? How can you rationalize your data? Why do we still have measles and rubella, but not polio and smallpox? Explain the relationship between the contact number and the fraction of immune individuals required for herd immunity in terms of the infectiousness of the disease - that is, use words, not mathematical symbols and formulas.
Of the diseases in the table, for which one does it appear hardest for a population to attain herd immunity?
What complications might exist in the real world when it comes to attaining the required fraction (hint: think about immunization and patient isolation techniques and how they may vary from one region of a country to another, and between countries)? In a free society, how much force can we use to require immunization?
In order to demonstrate just how problematic these complicating factors can be, consider the case of smallpox, which has the lowest contact number in our table.
Smallpox vaccinations began in 1958, but the disease persisted until 1977. How could you explain this? More important, what implications does this have for the likelihood of a population attaining herd immunity against a disease with a larger contact number?
3.4
Let's consider another complicating factor in reaching the required fraction of immune individuals.
Vaccines are not always effective - a small fraction of individuals who are vaccinated will not become immune.
About 15 to 20 years ago - a notable period in history - there were problems with measles vaccinations: the vaccines had a low "efficacy." The measure of a vaccine's effectiveness is its vaccine efficacy, VE. This is the fraction of vaccinations that result in immunity for the inoculated person.
Using this new parameter and your previous equation, determine the fraction of individuals who must be vaccinated (assuming your population consists entirely of susceptibles prior to immunization) to achieve herd immunity for the above diseases.
Now let's consider two specific cases, rubella and measles, which both have a vaccine efficacy of .95. Using the contact numbers given previously, compute the fraction of individuals who must be vaccinated in order to incur herd immunity.
What effect does the vaccine efficacy have on the likelihood of eradicating these diseases from the population? What are some techniques that could be employed to increase the population's chances of attaining herd immunity? (You may know that many universities require undergraduates to be revaccinated.)
The United States, rubella vaccination policy is an example of an attempt to vaccinate a high enough percentage of the population so that the disease will be held in check and, theoretically, herd immunity could be attained.
In order to carry out this policy, laws have been enacted that require children to have a rubella immunization prior to entering school - it is now estimated that 98 percent of the children entering school have been vaccinated.
As a result of this policy, the incidence of rubella in America has been steadily declining.
Can herd immunity be attained with this fraction of children being vaccinated? Upon what other factor(s) does the herd immunity depend? (hint: the immunizations began in 1969). The typical vaccine in this case is the MMR - measles, mumps, rubella booster.
From this fact, we can assume that about 98 percent of the children entering school have been immunized against measles, as well.
Is this fraction high enough to attain herd immunity?
There are social consequences of these health policies.
Some groups in our free pluralistic society do not believe in immunization.
Some groups do not want to create records of their existence.
How much social "leeway" does each vaccination strategy have?
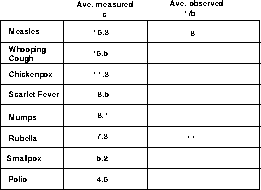
Figure 3.2: Table of Contact Numbers