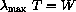
Hot bodies emit radiation. No, this isn't the start of a racy novel; we're referring to a blacksmith shop where iron comes out of the fire "white hot," cools to "red hot," and passes below the visible spectrum into the infrared. (Warm human bodies do emit infrared radiation, which is detected by the "motion" lights many of us have outside our houses.) Physicists wanted to be able to predict the "color" of radiation from the temperature.
Wien made measurements and found an empirical law that says: "When the absolute temperature of a radiating black body increases, the most powerful wavelength decreases in such a way that
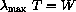
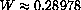 (cm
(cm K) is known as Wien's displacement constant.
K) is known as Wien's displacement constant.
Planck discovered a formula for the intensity of each frequency radiating from a black body. When we maximize intensity as a function of wavelength using Planck's formula we can derive Wien's law. This derivation was the first triumph of quantum mechanics. The classical theory made a wrong prediction and the new theory gave the right one and shows why Wien's law holds. We will show how Planck's law gives a theoretical derivation of Wien's law and how calculus, the computer and graphing interact in seeing this. We think this should show you why you should learn the rest of the chapter.
Planck began his study with a graph of the measured intensities, an empirical curve.
He then fit a formula to this curve in what his 1920 Nobel Prize lecture described as "an interpolation formula which resulted from a lucky guess." The lucky guess led him to a derivation from physical laws.
If you go to your local quantum mechanic's shop, just next door to the blacksmith, she will tell you that the intensity of radiation for the frequencies between
 and
and
 of a black body at absolute temperature T is
of a black body at absolute temperature T is

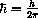 and
and
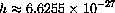 (erg sec) is called Planck's constant,
(erg sec) is called Planck's constant,
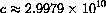 (cm/sec) is the speed of light, and
(cm/sec) is the speed of light, and
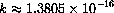 (erg/deg) is called Boltzmann's constant.
Physicists treat this formula as a differential because you need to measure a small range of frequencies, not just the intensity at one frequency.
(erg/deg) is called Boltzmann's constant.
Physicists treat this formula as a differential because you need to measure a small range of frequencies, not just the intensity at one frequency.
26.1
We want to be sloppy about the units in this example and just emphasize the difficulty we encounter because of the scales of the real physical constants.
Normally, we will not accept this practice ourselves or as part of your homework, but we don't want to get side-tracked with the physics.
The Feynman Lectures on Physics derive Planck's law (in angular frequency form) with their usual mixture of brilliance, charm and mathematical giant steps (flim-flam?). We won't repeat that.
If you wish to look that up, you can also straighten out the units and give careful definitions of the variables.
26.2
We want to express Planck's law in terms of wavelength
Let's take a hot object, say
The wavelength of red cadmium light in air is used for calibrations and equals
This plot tells us something, at least.
The interesting stuff must be between these ranges, so we try a range of {l,0,.002} in Figure 26.3.
Now we see what we want - the maximum.
It seems to be around 0.0003 as well as we can read the graph.
We didn't really use calculus, but a little physics to look for a reasonable range.
We were lucky to find the peak.
What we wanted was the place where the curve peaks, so we could have used calculus to find it.
And we can do that now.
Let
The graph is horizontal when
If we try to solve
The computer finds our root more accurately to be
We could try another value, say T=900, and work through the whole problem again, but that would just give us another specific number.
We need a formula that tells us how the maximum point depends on the temperature T. We can find this by solving the problem as before, but keeping the letter T as an unknown constant or parameter rather than letting T=1000.
26.3
The peak on each curve
What do we conclude? At the peak,
In summary, for fixed temperature, T, the maximum intensity occurs at the wavelength satisfying
You can work out the frequency form of Planck's law in PlanckF and compare it to the computer wavelength solution just described.
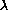 using the basic relation
using the basic relation
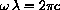
and its differential, so

giving
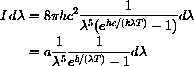
where
 and b=hc/k.
and b=hc/k.
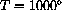 K (about
K (about
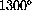 F). The first lesson the computer learns from hand computations is what range to plot.
Normally, in a textbook problem to plot a function like
F). The first lesson the computer learns from hand computations is what range to plot.
Normally, in a textbook problem to plot a function like
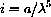 , you might pick a range like
, you might pick a range like
 . This is nonsense in our problem, because the interesting range of wavelengths is orders of magnitude smaller.
Let's try it with Mathematicain Figure 26.1 anyway:
. This is nonsense in our problem, because the interesting range of wavelengths is orders of magnitude smaller.
Let's try it with Mathematicain Figure 26.1 anyway: 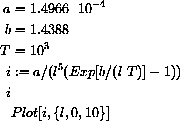

Figure 26.1: A useless plot
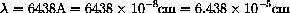
so let's try another range in Figure 26.2.
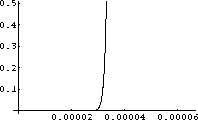
Figure 26.2: Also useless
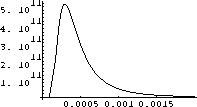
Figure 26.3: Intensity for
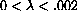
 , so
, so
 and use the Product Rule and Chain Rule:
and use the Product Rule and Chain Rule: 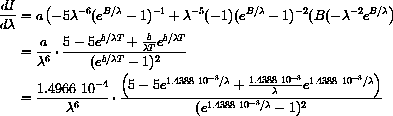
It is horribly messy to do this computation with the explicit values of the constants.
We want you to learn to use parameters, even in cases like this where they only make the calculations neater and thus easier to follow.
We will look at the computation with parameters below for a more important reason.
Actually, we asked you to differentiate Planck's formula in the last chapter and showed you the answer in the computer program Dfdx. All the computations in this section are on the program PlanckL and we encourage you to compare that with your Planck's law exercise below.
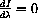 so the numerator must equal zero
so the numerator must equal zero
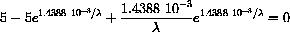
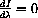 using the computer, we encounter nasty numerical problems because of the scale.
A change of variables makes the problem appear simpler and scales it in a form that the computer can handle.
Let
using the computer, we encounter nasty numerical problems because of the scale.
A change of variables makes the problem appear simpler and scales it in a form that the computer can handle.
Let
 and rewrite the equation above to obtain the problem:
and rewrite the equation above to obtain the problem: 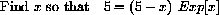
We need a starting guess at a root.
Figure 26.4 shows a root near x=5.
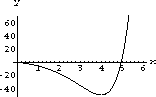
Figure 26.4: y=5-(5-x)Exp[x] 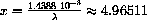 , so
, so
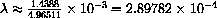 . The observed wavelength at 1000
. The observed wavelength at 1000 K is 0.000289782 cm.
Very nice start, but this is not the answer we are looking for.
We have only shown what happens at T=1000 and we want to know what happens as we vary T.
K is 0.000289782 cm.
Very nice start, but this is not the answer we are looking for.
We have only shown what happens at T=1000 and we want to know what happens as we vary T.
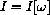 where T is constant (but not fixed at some specific number) still occurs the point where the slope is zero or
where T is constant (but not fixed at some specific number) still occurs the point where the slope is zero or
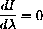
We want to solve the equation with the parameter T in the expression.
This isn't so hard given all our preliminary work.
We know

and the derivative is zero if the numerator is zero, or
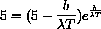
Substituting
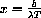 , we are left with exactly the problem we solved numerically above,
, we are left with exactly the problem we solved numerically above,

which holds when
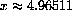 .
.
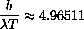
or
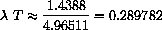
This is Wien's law,
 constant.
We have shown that the empirical law follows theoretically from Planck's quantum mechanical law and derived W=0.289782 versus the measured W=0.28978. The formulas are a little complicated and calculus plays a role in just finding plot ranges.
It plays an indispensable role in finding the formula for the peak by differentiating and solving with parameters.
constant.
We have shown that the empirical law follows theoretically from Planck's quantum mechanical law and derived W=0.289782 versus the measured W=0.28978. The formulas are a little complicated and calculus plays a role in just finding plot ranges.
It plays an indispensable role in finding the formula for the peak by differentiating and solving with parameters.
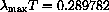
or
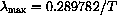 . The solution to the symbolic maximization problem gives us a function of the parameter T. This is a derivation of Wien's empirical law from Planck's theoretical law.
. The solution to the symbolic maximization problem gives us a function of the parameter T. This is a derivation of Wien's empirical law from Planck's theoretical law.
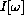 . Use the computer program PlanckF to help with the computations and sketch curves like the ones we have done for wavelength.
The intensity formula with frequency is
. Use the computer program PlanckF to help with the computations and sketch curves like the ones we have done for wavelength.
The intensity formula with frequency is
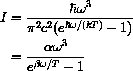
 on an appropriate range.
Figures 26.6 and 26.7 are two poor starting attempts:
on an appropriate range.
Figures 26.6 and 26.7 are two poor starting attempts:

Figure 26.5: A Bad Range of Frequency
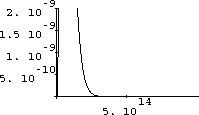
Figure 26.6: A Better Range
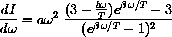
and show that this leads to the properly scaled root-finding problem
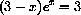
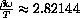 so
so
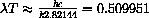 , since
, since
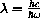 .
.