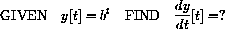
We start with the question
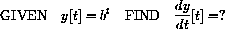
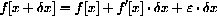
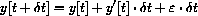
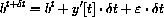
 unknown.
We solve for the unknowns, obtaining
unknown.
We solve for the unknowns, obtaining
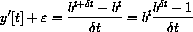
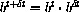 ). Assuming that
). Assuming that
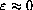 , we have
, we have
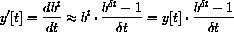
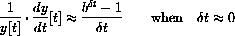
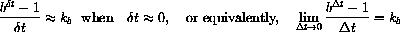

Begin your project with a derivation of this formula.
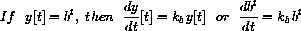
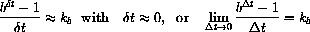
Next, use the computer to find a practical approximation to the constant k2. (Of course, we would also like to know the exact value of the constant, which turns out to be the natural base log of 2, 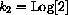 . The main text, Section 6.5, shows you the exact symbolic way to differentiate exponentials.)
. The main text, Section 6.5, shows you the exact symbolic way to differentiate exponentials.)
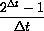
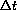 ; for example, you might let
; for example, you might let
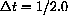 , 1/4.0, 1/8.0,
, 1/4.0, 1/8.0,  or
or
 , 0.01, 0.001,
, 0.01, 0.001,  . Notice that you cannot let
. Notice that you cannot let
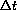 get "too" small and maintain numerical accuracy in a floating point computation.
get "too" small and maintain numerical accuracy in a floating point computation.
The program ExpDeriv on our website has help with these computations.
Compare your approximation with the computer's high-precision value of e. Your computation can only claim a reasonable amount of accuracy. How much is reasonable?
You can improve the accuracy by modifying the program to compute symmetric differences
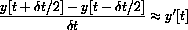
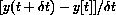 . Experimentally, you will see that this is more accurate.
The Mathematical Background chapter on Taylor's formula, Section 8.2, gives the mathematical reason for this accuracy.
. Experimentally, you will see that this is more accurate.
The Mathematical Background chapter on Taylor's formula, Section 8.2, gives the mathematical reason for this accuracy.
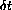 and
and
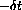 ,
, 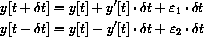
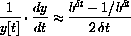
Use this formula to compute a table of closer and closer approximations to k2 and compare the accuracy with your first computation.
Once you have confidence in the accuracy of your tables of approximations for k2, compute tables of kb for the following exponential bases, b.
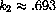 ,
, 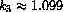 ,
, 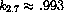 ,
, 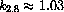 . Can you claim more accurate values for these constants with the computations in your program?
. Can you claim more accurate values for these constants with the computations in your program?
We haven't really proved that the limits defining the constants kb exist, but the numerical data from the the computer program are pretty convincing evidence that they do.
The meaning is quite important, namely we see that
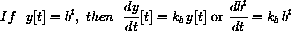
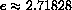 and it therefore satisfies the important identity
and it therefore satisfies the important identity
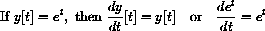
We use the relation
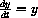 as a cornerstone of our "official" theory of exponentiation in the text.
The fact that the constant of proportionality is one for the base e is why e is considered the "natural" base for logs and exponentials.
This is somewhat like radian measure for angles, where at first you may prefer degrees but only get
as a cornerstone of our "official" theory of exponentiation in the text.
The fact that the constant of proportionality is one for the base e is why e is considered the "natural" base for logs and exponentials.
This is somewhat like radian measure for angles, where at first you may prefer degrees but only get
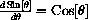 in radians.
in radians.
 . Explain.
Show that the derivative of the sine function in degrees is approximately 0.01745 times the cosine function in degrees.
. Explain.
Show that the derivative of the sine function in degrees is approximately 0.01745 times the cosine function in degrees.