
The use of "unknown functions" is of fundamental importance in calculus and other branches of mathematics and science. We shall often see in the course that differential equations can be viewed as identities for unknown functions. One reason that students sometimes have difficulty understanding the meaning of derivatives or even the general rules for finding derivatives is that those things involve equations in unknown functions. The symbolic rules for differentiation and the increment approximation defining derivatives are similar to general functional identities in that they involve an unknown function. It is important for you to get used to this "higher type variable," an unknown function. This chapter can form a bridge between the specific identities of high school and the unknown function variables from rules of calculus and differential equations.
In high school you learned that trig functions satisfy certain identities or that logarithms have certain "properties." All the the identities you need to recall from high school are



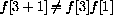 , so f[x]=x does not satisfy functional identity (ExpSum).
, so f[x]=x does not satisfy functional identity (ExpSum).
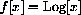 where x is any positive number.
Why does this f[x] satisfy the functional identities
where x is any positive number.
Why does this f[x] satisfy the functional identities


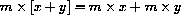

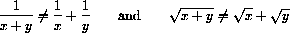
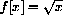 , the two sides are not equal.
Using the Mathematical Background book, Chapter 2, you can show that the only differentiable functions that do satisfy the additive functional identity are the functions
, the two sides are not equal.
Using the Mathematical Background book, Chapter 2, you can show that the only differentiable functions that do satisfy the additive functional identity are the functions
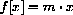 . In other words, the additive functional identity is nearly equivalent to the distributive law; the only unknown (differentiable) function that satisfies it is multiplication.
Other functional identities such as the seven given at the start of this chapter capture the most important features of the functions that satisfy the respective identities.
For example, the pair of functions f[x]=1/x and
. In other words, the additive functional identity is nearly equivalent to the distributive law; the only unknown (differentiable) function that satisfies it is multiplication.
Other functional identities such as the seven given at the start of this chapter capture the most important features of the functions that satisfy the respective identities.
For example, the pair of functions f[x]=1/x and
 do not satisfy the addition formula for the sine function, either.
do not satisfy the addition formula for the sine function, either.
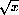 are not equal.
Show that 1/x and
are not equal.
Show that 1/x and
 also do not satisfy the identity (SinSum), that is,
also do not satisfy the identity (SinSum), that is,
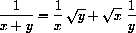
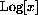 , but we don't know if f[x] is
, but we don't know if f[x] is
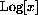 ), and suppose that f[0] is a well-defined number (even though we don't specify exactly what f[0] is). Show that this function f[x] must be the zero function, that is, show that f[x]=0 for every x. (Hint: Use the fact that 0*x=0.)
2) Suppose that f[x] is an unknown function that is known to satisfy (LogPower) for all x>0 and all k. Show that f[1] must equal 0, f[1]=0. (Hint: Fix x=1, and try different values of k.)
), and suppose that f[0] is a well-defined number (even though we don't specify exactly what f[0] is). Show that this function f[x] must be the zero function, that is, show that f[x]=0 for every x. (Hint: Use the fact that 0*x=0.)
2) Suppose that f[x] is an unknown function that is known to satisfy (LogPower) for all x>0 and all k. Show that f[1] must equal 0, f[1]=0. (Hint: Fix x=1, and try different values of k.)


 , f[x] will not satisfy (Mult) for all x (that is, given a nonzero b, there will be at least one x for which (Mult) is not true).
Prove that any function satisfying (Mult) also automatically satisfies the two functional identities
, f[x] will not satisfy (Mult) for all x (that is, given a nonzero b, there will be at least one x for which (Mult) is not true).
Prove that any function satisfying (Mult) also automatically satisfies the two functional identities


 , for some fixed number m (this is almost obvious).
Prove that a general power function f[x]=mxk, where k is a positive integer and m is a fixed number, will not satisfy (Mult) for all x if
, for some fixed number m (this is almost obvious).
Prove that a general power function f[x]=mxk, where k is a positive integer and m is a fixed number, will not satisfy (Mult) for all x if
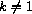 (that is, if
(that is, if
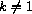 , there will be at least one x for which (Mult) is not true).
Prove that
, there will be at least one x for which (Mult) is not true).
Prove that
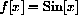 does not satisfy the additive identity.
Prove that f[x]=2x does not satisfy the additive identity.
In the early 1800s, Cauchy asked the question: Must a function satisfying
does not satisfy the additive identity.
Prove that f[x]=2x does not satisfy the additive identity.
In the early 1800s, Cauchy asked the question: Must a function satisfying

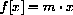 ? This was not solved until the late 1800s by Hamel.
The answer is "No." There are some very strange functions satisfying the additive identity that are not simple linear functions.
However, these strange functions are not differentiable.
? This was not solved until the late 1800s by Hamel.
The answer is "No." There are some very strange functions satisfying the additive identity that are not simple linear functions.
However, these strange functions are not differentiable.
Chapter 2, Functional Identities from the Mathematical Background book, Foundations of Infinitesimal Calculus, explores this problem in more detail.