Piecewise linear interpolation and bounds over large regions

For the finite element techniques we typically use piecewise linear functions: $a=x_0<x_1<\dots<x_{N-1}<x_N=b$, and the piecewise linear interpolant p(x) of s(x) is linear on each piece [x_i,x_i+1]. What we want is to bound the error e(x)=s(x)-p(x) or its derivative in either the $L^\infty$ or L² norms over [a,b].

To obtain these bounds, we need to combine the bounds on each piece into a bound over the entire interval. We can't do it all in one go over the entire interval, because $e^{\prime}$ is not absolutely continuous across the boundaries of the ``pieces''.

For the analysis, let h_i=x_i+1-x_i. Following the textbook, let h(x) = h_i for x between x_i and x_i+1.

We use the notation ||f||_L²(r,s) to denote the L² norm of f(x) over the interval (r,s) or [r,s]. Similarly, $\vert\vert f\vert\vert _{L^\infty(r,s)}$ is the maximum of |f(x)| over $r\le x\le s$.

$L^\infty$ bounds

We start with the bound (1) for

$$\vert\vert s-p\vert\vert _{L^\infty(r,s)} \le \frac18(s-r)^2 \vert\vert s^{\prime\prime}\vert\vert _{L^\infty(r,s)}$$

if p(x) is the linear interpolant of s(x) over the interval [r,s]. In particular, if (r,s)=(x_i,x_i+1),

$$\vert\vert s-p\vert\vert _{L^\infty(x_i,x_{i+1})} \le \frac... ...\vert h_i^2s^{\prime\prime}\vert\vert _{L^\infty(x_i,x_{i+1})}$$

and taking the maximum over $i=0,1,2,\dots,N-1$, we get

$$\vert\vert s-p\vert\vert _{L^\infty(a,b)} \le \frac18 \vert\vert h^2s^{\prime\prime}\vert\vert _{L^\infty(a,b)}.$$ (11)

If all we have is an L² bound on $s^{\prime\prime}$, then we use the piecewise bound (6) to get

$$\vert\vert s-p\vert\vert _{L^\infty(a,b)} = \max_i\vert\vert... ...rt{3}}\vert\vert h^{3/2}s^{\prime\prime}\vert\vert _{L^2(a,b)}.$$ (12)

L² bounds

If we wanted L² bounds we could use (7) to get

$$\begin{array} {rcl} \vert\vert s-p\vert\vert _{L^2(a,b)}^2 ... ...t\vert h^2s^{\prime\prime}\vert\vert _{L^2(a,b)}^2.\end{array}$$

and so

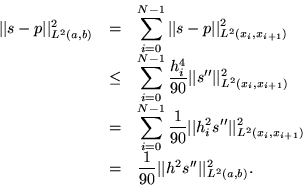
$$\vert\vert s-p\vert\vert _{L^2(a,b)}\le \frac{1}{\sqrt{90}} \vert\vert h^2s^{\prime\prime}\vert\vert _{L^2(a,b)}.$$ (13)

Derivative bounds

We can use (9) to obtain over-all bounds on ||s'-p'||_L²(a,b):

$$\begin{array} {rcl} \vert\vert s'-p'\vert\vert _{L^2(a,b)}^... ...vert\vert hs^{\prime\prime}\vert\vert _{L^2(a,b)}^2\end{array}$$

and

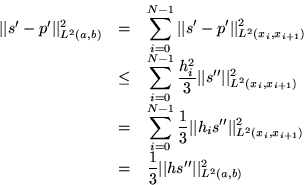
$$\vert\vert s'-p'\vert\vert _{L^2(a,b)}\le\frac1{\sqrt{3}}\vert\vert hs^{\prime\prime}\vert\vert _{L^2(a,b)}^2.$$ (14)