A new breakfast roll called `Byties' becomes popular in our community.
There is no patent on Byties, so anyone who chooses may decide to bake them. (Unlike a monopoly.) The price at which Byties sell determines who bakes Byties and how many they bake on a given day.
At a high price, more people are willing to get up at 3:00 am, make the batter, and bake the rolls, so supply is an increasing function of price.
For simplicity, we begin with the idealized assumption that the aggregate supply function is linear. "Aggregate supply" means that we don't know exactly who bakes the Byties but rather only know that the community's supply quantity, q, is given by
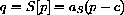
where c is the unit cost of ingredients, baking energy, etc., and aS is a positive constant determined by the aggregate of bakers. For example, if the cost of producing one Bytie is 40 cents and aS=1000, then S[p]=1000(p-.40)=1000p-400 (for p in dollars) as in the first example of Chapter 20. It is still useful to write supply in the form 1000(p-.40) because it tells us the cutoff point for bakers. No one will bake at a loss, so if the price drops below the cost of production, supply is zero. In other words, q=S[p]=aS(p-c) for
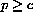and S[p]=0 otherwise.
Similarly, our mythical community has a linear aggregate demand function.
The total number of Byties purchased on a given day is given by
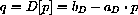
for positive constants aD and bD. Again, there are implicit constraints. No one sells at negative prices, so the function is only economically defined for
and, in practice, really only for
. Similarly, negative demand does not make sense, so there is an upper limit on the price our market will bear.
Basic discussion and understanding of your economy can begin with the specific case studied in Chapter 20
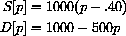
but should strive to understand the role of the general parameters.
Describe the basic model, give the variables with units, and describe the role of the various parameters (aS, c, aD, aS). The unit cost c is easy to explain, but you can at least say what large values of aS mean about your economy. Other meaning may be derived indirectly. For example, what is the maximum price the market will bear in terms of the parameters you have chosen? Does the demand function represent the wishes of every individual separately (multiplied by the number of people) or only the overall impact? For example, does the model say whether everyone buys twice as many Byties at 50 cents as at 1 dollar, or that more people buy at the lower price?
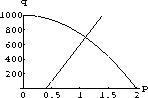
When supply equals demand, all the rolls are sold for producers willing to bake at that price and all the consumers willing to pay the price are satisfied. This is an equilibrium between the aggregates of producers and consumers.
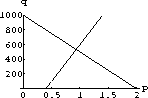
Figure 29.1: Supply and Demand for Byties
What is the equilibrium price in terms of the parameters of your model? pe=? The formula is easy and you will probably want to include this fundamental computation in your computer program so you can see the specific output for each choice of parameters. You could be lazy and ask the computer to solve the equations.
We have given you a start at the computations in the computer program BytieHelp on our website.
When demand exceeds supply, such as when all the rolls are sold well before breakfast time is over, there is incentive for more bakers to bake and charge a higher price.
Our model economy adjusts price by making the change in price proportional to the amount by which demand exceeds supply.
Suppose today's price is p[t] and the excess demand D[p[t]]-S[p[t]] is positive.
The change in price for tomorrow, p[t+1]-p[t], is a constant times the excess demand, so
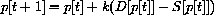
where k is a positive constant.
What does the model say happens if supply exceeds demand?
Explain how the model predicts a sequence of daily prices, once you are given a starting price, that is, how an initial price p[0]=P0 together with the change equation above determines a whole infinite sequence of prices {p[0],p[1],p[2],p[3],...}. Does this basic determination require that supply and demand are linear? When they are linear, is there a closed formula for the value of the price on day t?
What is the importance of the parameter k for the stability of the breakfast economy of your mythical community? Use the computer program BytieHelp to compute and graph some examples where k is small and prices above equilibrium adjust downward toward a limit
or prices below equilibrium adjust upward toward the equilibrium price. Give larger examples of k where prices oscillate above and below equilibrium, but still tend to equilibrium in the long term. Finally, give values of k where prices do not tend toward equilibrium. Figure 29.5 shows an example with k=0.0013 showing both the cobweb and the explicit graph.
Use the Linear Stability Theorem of Chapter 20 to give a condition on your parameters to guarantee that every initial price results in a price sequence satisfying
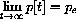
What is the best combined measure of stability for your economy? How do the parameters k, aS, aD, etc. affect the stability of the economy? Large values of aS mean that producers are very responsive (why?), but does that make the economy more or less stable? Large values of aD mean that consumers are very price sensitive (why?), but does that make the economy more or less stable? What combination of these sensitivities makes for a stable price sequence? Does the unit cost of production c affect the stability? Does it affect the limiting price?
29.2
29.3
Your school wants to keep tuition down but must pay its bills and decides to put a tax on the popular new Byties.
This increases the cost of production from c1 to c2. For example, in the numerical case at the beginning of the project you might consider the change from S[p]=1000(p-.40) to S[p]=1000(p-.45).
A natural question, even in this specific case, is, What happens to profits? The total profit before is the unit profit p-c1 times the number sold at price p. The number sold is the demand, so total daily profit is ???
What is the effect of the change in c on the quantity sold at equilibrium? (Hint: Show that
Can a change in price affect the stability of the economy? For example, could the economy stably approach the first equilibrium price, but become unstable after a change from c1 to c2?
What is the effect of the change in c on profit at equilibrium prices? You can express the equilibrium profit in terms of the parameters and consider it a function of c, Profit[c] = ? What are the maximum and minimum of this function?
The previous exercise shows that the tax increases equilibrium price, decreases equilibrium demand, and decreases profit.
The next question is, Who pays? The tax collected at equilibrium is (c2-c1)D[pe2] and the change in profit is Profit[c1] - Profit[c2].
29.5
Finally, we come to the questions concerning the addition of a tax on Byties.
Begin your work with the following two experiments.
You will observe stability at 30 cents and instability at 50 cents.
Why is this (mathematically and economically)?
What is the equilibrium profit at a unit cost of 30 cents?
What is the total tax collected if 20 cents is added to the 30 cent cost?
What is the profit at a unit cost of 50 cents?
How does the drop in profit from 30 to 50 cent costs compare with the total tax collected?
Conclude your project on the Bytie economy with some general comments about the difference between linear and nonlinear models.
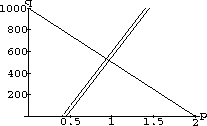
Figure 29.2: A Cost Increase
Add a computation to your computer program to compute the sequence of daily profits.
What happens to profit for a 5 cent tax on Byties in the basic numerical case?
Figure 29.3: Daily Profits at c=.40
When unit cost is increased from c1 to c2, what is the resulting change in equilibrium price, pe1 to pe2?
.)
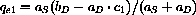Compare the loss of profit with the total tax collected.
The initial price was
$1.50 and the factor for rate of adjustment was k=0.0013.
Let k=0.0013, aS=1000, aD=250, bD=1000 and compute the equilibrium price and some price sequences for the two cases:
c=.30
c=.50
