Calculus: Project 19

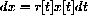
The differential equation dx=rx[t]dt has solutions of the form x[t]=x₀e^rt when r is constant. (See the main text, Section 8.2.) This project shows that you can still solve a differential equation that is "linear in x,"

One "method" is by guessing that the solution has the form

for some unknown function R[t].

Let x[t]=x₀e^R[t], for a constant x₀ and unknown function R[t]. Use the Chain Rule to show that

provided R'[t]=r[t] or .
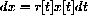
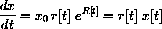
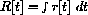In particular, show that when , x[t]=e^t²/2 sartisfies

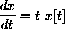
Another method of solution is called "separation of variables" and is studied in Chapter 21 of the main text. Here is how that works in this case:

Write the differential equation

and antidifferentiate both sides with respect to the separate variables,

Solve for x and show that you get the solution

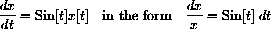
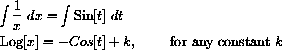
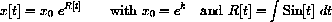
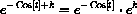(Hint: Why does ? If k is an arbitrary constant, so is e^k - except for sign.)

Verify by substitution that 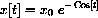satisfies the differential equation for any value of the constant x₀.

Differential equations say how a quantity changes with time. In order to know "where we end up," we need to know where we start.

Solve the initial value problem

(Hint: The derivative of is 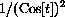. What is x[0] if ?)

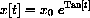Once we know how to solve dx=r[t]dt, we can solve the "forced" equation by the unlikely method called "varying the constant." Here's how that works for the "forcing" function f[t].

Suppose we are given the functions R[t] and r[t] where x[t]=e^R[t] is a solution of dx=r[t]x[t]dt, that is, R'[t]=r[t]. We want to solve the equation

"Guess" the solution x[t]=c[t]e^R[t] and substitute it into the equation. Use the Product Rule and Chain Rule to show that

This "guess" will work provided

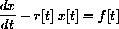
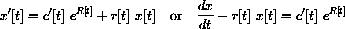
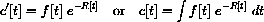
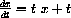Test this "guess" on the equation where r[t]=t and R[t]=t²/2. Compute

Show that this makes

and substitute it in the differential equation to verify that it is correct.

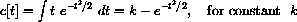
The exact differential equation solvers in Maple and Mathematica will also solve these equations.

Previous project Next project Close this window