Calculus: Project 13

We want to find the shape and length of electrical wires hanging between telephone poles. Intuitively, we know that we cannot stretch the wire perfectly straight, because there has to be some upward component of the tension force to counteract the weight of the wire and hold it up. The total length is one component of the cost in hanging such wires, but the strength of the wire is a counterbalancing cost. If we want to make the wire very nearly straight, then we need to make it very strong to support the tension required in straightening it. We will develop a model that has an optimal shape (or amount of sag) in terms of the tension (that is, minimal required strength). Our model is based on two simplifying assumptions:

13.1 The Catenary Hypotheses

1. The wire is perfectly flexible, that is, supports no bending forces.

2. The wire is perfectly inelastic, that is, does not stretch. Catena in Latin means "chain." A chain is very strong, so it does not stretch very much, and because of the links, it does not support any bending force beyond a single link. We may imagine that our model curve is a chain made of infinitely strong infinitesimal links. The center line of this chain is the curve we seek to describe.
There are two parameters in our model, the linear density of the chain and the horizontal force at the pole. Imagine hanging the chain by hanging it over the poles and then pulling on it to shorten the sag. The pulling force is H. The weight of the chain is a function of its length.
13.2 Parameters

1. w - the linear weight density (n/m) of the chain.
2. H - the horizontal tension in the chain at the pole in newtons. The m-k-s unit of force is "newtons." A copper wire 1 cm in diameter weighs about 5 n/m. (A mass of 1 kilogram weighs g=9.8 n.) Linear weight density means that a chain L meters long weighs 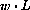newtons.

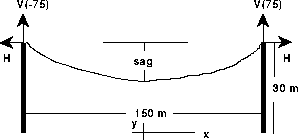
Figure 13.1: A Catenary Suspended over 30-m Poles 150 m Apart
We place an (x,y)-coordinate system on the ground below the low point of the catenary.
13.3 Variables

1. x - the distance measured horizontally to a point on the catenary (m)
2. y - the distance measured vertically from the ground to a point on the catenary (m)
3. L - the length along the catenary from 0 to x (m)
4. T - the total tension vector above x (n)
5. V - the horizontal component of tension above x, T(x)=(H,V(x)) (n)
13.4 The Equation for Tension
A hanging electrical wire remains at rest, so its velocity and acceleration are zero. Newton's F=mA law implies that the total force must also be zero, or that the tension forces and gravity must sum to zero. A rough sketch of a segment of wire is shown in Figure 13.2. We imagine cutting out a segment and holding the ends at the tension that would normally be present keeping it stationary.
The fact that the catenary does not move left or right means that the horizontal acceleration is zero and the horizontal forces cancel, so H is constant or H(x)=H(x+dx), for any size x and dx. There are three vertical forces on a piece of the catenary, the upward pull at x+dx, the downward pull at x and the weight acting down. "No vertical motion," means that the total force up must equal the total force down, or

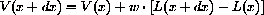
for any size x and dx along the catenary. This functional identity may also be written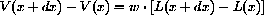 , the change in vertical force equals the change in weight.
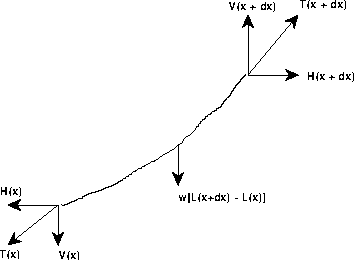
Figure 13.2: Tension on a Small Segment
To find a differential equation for the vertical tension, we will examine a small increment of the catenary. If the catenary is a differentiable curve, the Increment Principle (see Chapters 3, 4, 5, and 18 of the main text) says that the magnified curve will appear to be a straight line, so if we mark changes in x and y on the microscopic view, we will see a triangle. This triangle tells us two things; (1) the approximate length of an increment and (2) the relation between the components of tension and the slope.

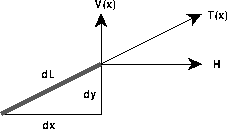
Figure 13.3: A Tiny Increment of the Catenary
The length of the portion of the catenary is then given by the Pythagorean theorem, since the catenary forms the hypotenuse of the apparent triangle.

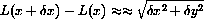
Actually, we should be a little more precise about the approximation. What we know is that the error is small on the scale of the microscope, or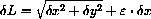

with .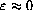
Since the catenary cannot support any bending force, the tension force must act tangent along the catenary or the finite size horizontal and vertical components of tension must form a triangle similar to the increment triangle. In other words, the slope of the curve must equal the slope of the tension triangle,

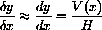
The equation that says there is no vertical motion applies to the small increment (by the Function Extension Axiom) to tell us

The Vertical Tension
Show that the vertical component of the tension in a catenary satisfies the initial value problem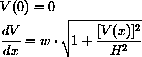

Why is the vertical tension zero at the bottom of the catenary?
Show that the unique solution of this problem is

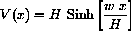
In other words, show that substitution of this function satisfies the differential equation and initial condition. Does this initial value problem satisfy the hypotheses of Theorem 17.20 of the main text?
See Exercise 18.33 of the main text for more on "hyperbolic trig functions." The basic facts are

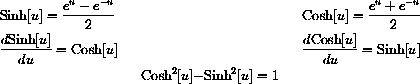
The Position
Show that the differential equation for y=y(x) along the catenary is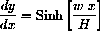

so that, we can write y(x) in the form

where y(0)=Y₀. (Hint: How much are and ?)
Use Mathematicato plot y(x) when w=5, H=1000, and Y₀=20.

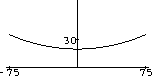
Figure 13.4: Hyperbolic Cosine
There is a problem with the expression that we have given for the position of the catenary. We want to have 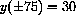, so that the wire is at the top of the poles when 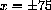. We also know that we physically adjust the amount of sag in the catenary by pulling on the chain or changing H. In other words, we do not know Y₀, but set it by finding H.

The Sag
Show that the sag in the catenary satisfies the equation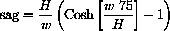

(Hint: How much is y(75)-y(0) even if you do not know y(0)?)
Given a catenary with w=5, find the horizontal tension H needed to produce a sag of 10 m. Use Mathematica's root finding command, FindRoot[ y == s,{h,1000}] FindRoot[] approximates a root to the equation y=s given an initial guess of h=1000. Once you have found the correct tension, find the equation for the catenary and Plot your result. (As a check, how much is y(0)?)
The strength needed in the catenary is governed not just by the vertical component of the tension but rather by the magnitude of the whole tension vector.

The Highest Tension
Show that the magnitude of the tension vector at any point x along the catenary is given by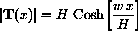

(Hint: Use the identity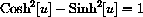 and the two components of tension.)
Prove that the maximum tension occurs at the endpoint,

and use this to find the maximal tension in the catenary with w=5 and a sag of 10 meters in 75.
Now that we know the strength required to make a catenary with a sag of 10 m in 75, we want to find its length. We saw above in this section (and in Chapter 14 of the main text) that the length of a tiny piece of the catenary is

Hence, the length of the catenary is given by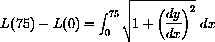

The Length
Show that the length of the catenary from the low point at x=0 to the pole at x=75 is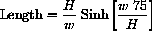

(A shortcut to integration would be to compare the total weight to the upward force at the pole.) Use this to calculate the length of a catenary with w=5 and a 10-m sag in 75 meters.
13.5 Optimizing Length and Strength
Intuitively, we know that we cannot stretch the catenary perfectly straight between the poles. Verify this mathematically:

The Limit as or sag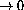
Prove that it requires huge maximum total tension, |T(75)|, to make a catenary with a tiny sag, or if sag, then H must be infinite. (Hint: Use the equation relating H to sag.)
The previous exercise shows that some sag is desirable for chains of finite strength, but it should also be clear that the sag should not be too big. In fact, even neglecting the fact that the catenary would touch the ground unless the poles were made taller, a very long cable produces very high weight.

The Limit as 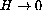or sag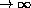
Prove that it requires huge maximum total tension, M=|T(75)|, to make a catenary with a huge sag, or if sag is infinite, then M=|T(75)| must be infinite. (Hint: Use the mathematical connection between length, weight, and maximum tension.)
If we combine the results of the last two exercises, we see that the graph of M comes down from infinity as H moves away from zero and that the graph goes back to infinity as H goes to infinity.

Plot the maximal tension M as a function of H using Mathematica for the specific parameter w=5 and the pole at x=r=75.
Show that each catenary has an optimal sag, that is, a sag and associated horizontal tension H so that the maximum total tension at the pole is minimal among all such catenaries.
How can you find symbolically in terms of the parameters?
If you want to hang a chain with w=5 in such a way as to minimize the strength required to support it, how much sag do you allow in 75 m?

Previous project Next project Close this window