Advanced Calculus using Mathematica
Advanced Calculus using Mathematica: NoteBook Edition is a complete text on calculus of several variables written in Mathematica NoteBooks.
Implicit 2D: Procedure 4.2.1
The Theorem on Smooth Formulas 3.3.1 is easy to apply and it tells us that this microscopic view is true. It boils down to a procedure: compute and check that your computation makes sense. To prove smoothness when the coordinate function is given by a classical formula, verify that the formulas f[x,y], ![]() , and
, and ![]() are valid in a rectangle about our particular point of tangency, X(x,y).
are valid in a rectangle about our particular point of tangency, X(x,y).
Procedure 4.2.1: Finding the Implicit Tangent Line
Suppose f[x,y] is smooth in a neighborhood of a particular fixed X=X(x,y). To find the equation of the line tangent to the implicit contour curve ![]() , at X=X(x,y), for
, at X=X(x,y), for ![]() constant, do the following steps:
constant, do the following steps:
1. Compute the general total differential of the equation ![]()
![]()
(the coefficients ![]() , and
, and ![]() are functions of x and y)
are functions of x and y)
The right hand side is zero since the partial derivatives of a constant ![]() are zero.
are zero.
2. Calculate the specific values of the partial derivatives at the particular X(x,y), ![]() and
and ![]() , verify that at least one partial derivative is not zero, and write the specific total differential at this point:
, verify that at least one partial derivative is not zero, and write the specific total differential at this point:
m·d x+n·d y=0 or G • d X =0
(the coefficients m and n are specific numbers)
3. (Optional) If you want the equation of the tangent line in (x,y)-coordinates, do the following. Say ![]() is your particular point of tangency. The local (d x,d y)-coordinates are related to (x,y)-coordinates by
is your particular point of tangency. The local (d x,d y)-coordinates are related to (x,y)-coordinates by ![]() and
and ![]() , so replace d x with
, so replace d x with ![]() , and d y with
, and d y with ![]() , obtaining the equation:
, obtaining the equation:
![]()
The result of Step 2 is an implicit line through the (d x,d y)-origin with perpendicular ∇f[x,y]. You can plot the tangent line using this equation in local coordinates (d x,d y) centered at the particular (x,y). The equation says, “An unknown vector d X =(d x,d y) (with origin at the point of tangency X(x,y)) lies on the tangent line provided it is perpendicular to the particular gradient G(m,n).”
The result of Step 3 is an implicit line through the point ![]() with perpendicular
with perpendicular ![]() . This equation says, “An unknown vector X (with origin at (x,y)=(0,0)) lies on the tangent line provided its displacement from
. This equation says, “An unknown vector X (with origin at (x,y)=(0,0)) lies on the tangent line provided its displacement from ![]() is perpendicular to the particular gradient G(m,n).” Notice that to correctly evaluate this final expression, you need to perform steps (1), (2), and (3) in that order.
is perpendicular to the particular gradient G(m,n).” Notice that to correctly evaluate this final expression, you need to perform steps (1), (2), and (3) in that order.
When ![]() , the implicit equation does not define a line. The explicit graph z=f[x,y] has a horizontal tangent plane at a point with zero gradient, but the level set f[x,y]=c may be a curve that does not have a tangent (or other things). We take this up in the subsection below and in Chapter 5 on Implicit and Inverse Functions. The rigorous basis for this procedure is in Theorem 5.2.2 below. It says, if you can compute the tangent line, then the contour is a smooth curve near the point of tangency.
, the implicit equation does not define a line. The explicit graph z=f[x,y] has a horizontal tangent plane at a point with zero gradient, but the level set f[x,y]=c may be a curve that does not have a tangent (or other things). We take this up in the subsection below and in Chapter 5 on Implicit and Inverse Functions. The rigorous basis for this procedure is in Theorem 5.2.2 below. It says, if you can compute the tangent line, then the contour is a smooth curve near the point of tangency.
Find the line tangent to the contours of ![]() at (2,1), (-1,2), and (-2,-1).
at (2,1), (-1,2), and (-2,-1).
Solution at X(2,1)
Step 1: The contour ![]() has symbolic total differential
has symbolic total differential
![]() and symbolic gradient
and symbolic gradient 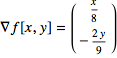
The function and partial derivatives are defined everywhere, so the function is smooth.
Step 2: At (x,y)=(2,1), the specific total differential is
![]() with specific gradient
with specific gradient ![]()
We sketch this line on the contour plot of the function by drawing the gradient vector with its tail at the point (x,y)=(2,1) and filling in the perpendicular line as shown next.
Figure 4.4.2: Contour Plot of ![]() and the tangent line at (2,1)
and the tangent line at (2,1)