 is smooth in a neighborhood of a particular fixed (s,t) and
is smooth in a neighborhood of a particular fixed (s,t) and
Advanced Calculus using Mathematica
Advanced Calculus using Mathematica: NoteBook Edition is a complete text on calculus of several variables written in Mathematica NoteBooks.
Parametric 2D: Procedure 15.3.1
Here is the general procedure for finding the tangent to a parametric surface:
Procedure 15.3.1: Finding a Parametric Tangent Plane
Suppose  is smooth in a neighborhood of a particular fixed (s,t) and
is smooth in a neighborhood of a particular fixed (s,t) and ![]() . To find the equation of the plane tangent to the parametric surface X[s,t] at (s,t) do the following steps:
. To find the equation of the plane tangent to the parametric surface X[s,t] at (s,t) do the following steps:
1. Compute the general symbolic derivatives ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and total differential:
and total differential:
![]() or
or 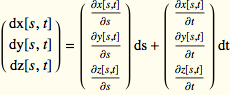
(The derivatives are functions of (s,t).)
2. Calculate the specific values of the derivatives at the particular (s,t), ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and write the specific total differential at this point:
, and write the specific total differential at this point:
dX = U ds+V dt or 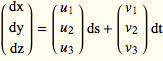
This is the equation of the parametric plane through the dX-origin with directions U and V and parameters ds and dt.
3. (Optional) If you want the equation of the tangent plane in (x,y,z)-coordinates, say ![]() ,
, ![]() ,
, ![]() is your particular point of tangency and
is your particular point of tangency and ![]() ,
, ![]() ,
, ![]() and
and ![]() ,
, ![]() ,
, ![]() are your two particular tangent vectors. The local (dx,dy,dz)-coordinates are related to (x,y,z)-coordinates by
are your two particular tangent vectors. The local (dx,dy,dz)-coordinates are related to (x,y,z)-coordinates by ![]() ,
, ![]() , and
, and ![]() , so replace dx, dy, and dz with
, so replace dx, dy, and dz with ![]() ,
, ![]() , and
, and ![]() , obtaining the equation
, obtaining the equation
![]() or
or ![]() or
or 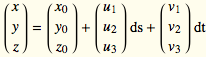
This is the parametric plane through ![]() with directions
with directions ![]() and
and ![]() and parameters ds and dt. Notice that to correctly evaluate this final expression, you need to perform steps (1), (2), and (3) in that order.
and parameters ds and dt. Notice that to correctly evaluate this final expression, you need to perform steps (1), (2), and (3) in that order.
You can plot the tangent plane using the equation in local coordinates (dx,dy,dz) centered on the surface at the particular X[s,t]. The graph of this equation is a parametric plane through the (dx,dy,dz)-origin centered at the point X[s,t].

Figure 15.3.5: The Plane Tangent to a Parametric Surface
The procedure breaks down if U and V are scalar multiples because the parametric graph of ![]() is not a plane, but rather lies on a line thru
is not a plane, but rather lies on a line thru ![]() in the direction of U,
in the direction of U, ![]() ,
, ![]() or is just a point if both tangent vectors are zero.
or is just a point if both tangent vectors are zero.
Find the equation of the plane tangent to the unit sphere at (s,t)=(π/4,π/3)
 , 0<s<π, 0≤t≤2 π, and
, 0<s<π, 0≤t≤2 π, and 
Step 1:
 &
& 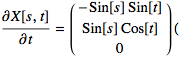
and all three vectors are defined for all (s,t), so the functions are smooth. They are non-parallel for 0<s<π by the cross product computation in Example 15.4.2, 3.
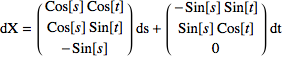
Step 2:  &
& 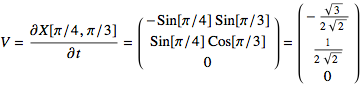
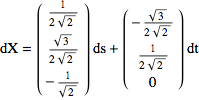 or
or
Step 3:
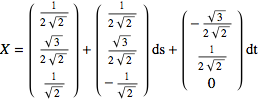 or
or 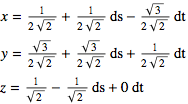
You sketch the plane in local coordinates by drawing the two tangent vectors and filling in the plane as above in Figure 15.4.6
Perpendicular ("normal") to a parametric surface
The cross product ![]() is perpendicular to both
is perpendicular to both ![]() and
and ![]() , hence is perpendicular to the tangent plane and the surface. (The perpendicular to a surface is sometimes called the “normal” vector to the surface.) In the example of the unit sphere at (s,t)=(π/4,π/3),
, hence is perpendicular to the tangent plane and the surface. (The perpendicular to a surface is sometimes called the “normal” vector to the surface.) In the example of the unit sphere at (s,t)=(π/4,π/3),
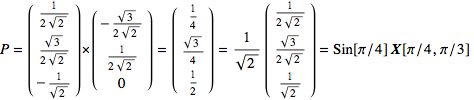
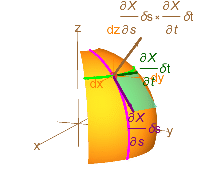
Figure 11.11.6: The Perpendicular to the Plane Tangent to a Parametric Surface