NSF Focused Research Group:
Wavelets, Frames, and Operator Theory
This FRG will enhance collaboration among the members by:
-
holding regular think-tank-style workshops,
-
involving students and postdocs in those workshops,
-
exchanging students for short visits among the Principal Investigators,
-
forming project subgroups to attack specific problem areas.
Contents
A sample of the FRG research problems
Project areas
Participants
Events (upcoming events in red)
Reports
A sample of the FRG research problems:
-
Definition:
A subset
  is said to be a wavelet set for an expansive integral
is said to be a wavelet set for an expansive integral
 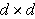 matrix
matrix
 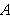 if the inverse Fourier transform
if the inverse Fourier transform
  of
of
 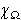 is a wavelet, i.e., if the double indexed family
is a wavelet, i.e., if the double indexed family
 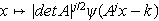 , ,
 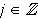 , ,
 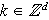 ,
is an orthonormal basis for ,
is an orthonormal basis for
  .
(This is equivalent to .
(This is equivalent to
  tiling
tiling
 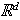 both under the translations
both under the translations
 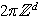 and the scalings
and the scalings
 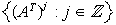 .) .)
-
Problem A: Wavelet set implementation. Because of the structure of wavelet
sets, their explicit constructions, and the potential usefulness of dealing
with only one wavelet in higher dimensions, there are two immediate and
natural problems. We wish to develop recursive programmable schemes for
applications, cf. [BT93, Stro00a, Wic94], as well as a theoretical formulation
in terms of frames, cf. [HL00, Han97].
This latter approach would sacrifice orthonormality, which is often not a
sacrifice in applications dealing with noise reduction and stable
representation. On the other hand, the frame theoretic approach would reduce
the recursive complexity, it would add smoothness in the spectral domain, and
it would provide an iterative method of signal reconstruction. Related to this
whole issue is the necessity of a critical comparison of the geometrical
constructions in [BS01] and the theoretical but constructive approach in
[BMM99] in terms of multiplicity functions and finite von Neumann algebras.
Further, the examples of wavelet sets are typically fractal-like, in the sense
that the sets are given as limits of infinite processes. Numerically, this
could pose difficulties. Consequently, one may seek wavelet sets that are, for
example, finite unions of rectangles. In this regard, Merrill has discovered a
family of multiwavelets (with multiplicity 2 in 2 dimensions) of this type,
cf. the geometric examples after the complete iteration in [DL98].
[BMM99] L.W. Baggett, H. A. Medina, and K. D. Merrill, Generalized
multi-resolution analysis, and a construction procedure for all wavelet sets
in Rn, J. Fourier Anal. Appl., 5 (1999), 563-573.
[BS01] J. J. Benedetto and S. Sumetkijakan,
A fractal set constructed from a class of wavelet sets,
Inverse problems, image analysis, and medical imaging (New Orleans, LA, 2001)
(M. Zuhair Nashed and Otmar Scherzer, eds.),
Contemporary Mathematics, vol. 313,
American Mathematical Society, Providence, RI, 2002,
pp. 19-35.
[BT93] J. J. Benedetto and A. Teolis, A wavelet auditory model and data
compression, Appl. Comput. Harmon. Analy., 1 (1993), 3-28.
[DL98] X. Dai and D. R. Larson, Wandering vectors for unitary systems and
orthogonal wavelets, Mem. Amer. Math. Soc., 134 (1998), no. 640.
[Han97] B. Han, On dual wavelet tight frames, Appl. Comput. Harmon. Anal., 4
(1997), 380-413.
[HL00] D. Han and D. R. Larson, Frames, bases and group representations, Mem.
Amer. Math. Soc., 147 (2000), no. 697.
[Stro00a] T. Strohmer, Numerical analysis of the non-uniform sampling problem,
J. Comput. Appl. Math., 122 (2000), 297-316.
[Wic94] M. V. Wickerhauser, Adapted Wavelet Analysis from Theory to Software,
A K Peters Ltd., Wellesley, MA, 1994.
-
Definition:
(see [JoPe92]) A measurable set
  in
in
 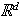 ,
of finite positive measure, is said to be a spectral set if ,
of finite positive measure, is said to be a spectral set if
 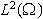 has an orthogonal basis of real exponentials
has an orthogonal basis of real exponentials
 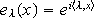 for a subset
for a subset
 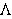 of points
of points
 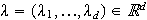 .
If an orthogonal basis .
If an orthogonal basis
  exists,
exists,
  is called a spectrum.
is called a spectrum.
  is said to be a tiling if it can be made to tile
is said to be a tiling if it can be made to tile
 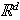 using only translations.
[JoPe92]
P. E. T. Jorgensen and S. Pedersen, Spectral
theory for Borel sets in
using only translations.
[JoPe92]
P. E. T. Jorgensen and S. Pedersen, Spectral
theory for Borel sets in
 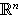 of finite measure, J. Funct. Anal., 107 (1992), 72-104.
of finite measure, J. Funct. Anal., 107 (1992), 72-104.
-
Problem B: Spectra-Tilings Conjecture.
Let
 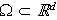 with
with
 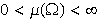 .
If .
If
  is a spectral set, then
is a spectral set, then
  tiles
tiles
 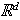 by translation. Further, there is a one-to-one correspondence between the
spectra of
by translation. Further, there is a one-to-one correspondence between the
spectra of
  and the set of tilings of
and the set of tilings of
  . .
The Fuglede conjecture, in its original primitive form, is 40 years old, but
it has come to signify a much more general principle: It is now used to
describe any one of several correspondences between spectrum and geometry, much
in the spirit of Mark Kac's "Can you hear the shape of a drum?" theme. In its
original form, the Fuglede conjecture states that an open set S of finite
positive measure in Rd admits a Fourier basis F if and only if it tiles Rd
with translations. This form of the conjecture is still open, but it is
recognized as being difficult, involving combinatorics and number theory. A
number of serious attempts at counterexamples have not succeeded. But in many
applications, more detailed information is available about the context of the
problem: If for example S is known to be the finite union of non-overlapping
intervals, then the possible spectral pairs (S,F) are of significance in
combinatorics and in sampling problems. Therefore much effort in the FRG has
been focused on cases when S is already known to satisfy both the basis
condition and the tile condition. Then the question is the correspondence
between spectrum and tile-translations, or more generally between spectrum and
geometry. This is "the generalized Fuglede conjecture", and it has been
extraordinarily fruitful. The simplest case arises when the vectors that
produce a Fourier basis are also translation vectors in a tiling. Several of
us in the FRG have published papers on this: For example, if S is the d-cube,
members in the FRG and their co-workers showed that the frequencies F in a
Fourier basis and the vectors V that make S tile coincide, i.e., F = V, and
when d = 3, we found the possibilities for F. Equivalently, (S,F) is a
spectral pair if and only if (S,F) is a tile system. But spectral/tile duality
is a central theme in many wavelet problems, in iterated function systems, in
spectral theory for Hilbert spaces built from Hausdorff measure Hs, of
fractional dimension s.
They are
central in
harmonic analysis,
see for example
the websites of
Terence Tao
and
I. Laba,
and this
FRG website.
In its general form, the Fuglede
conjecture is central to how we construct wavelet bases, and Gabor frames. In
the FRG,
Jorgensen
and his Ph.D. student
D. Dutkay
proved that the spectral/tile
principle applies to Hs, Hausdorff measure,
0 < s < 1, and that the duality
principle lets us write down wavelet bases in Hs-Hilbert spaces. Even for
the middle-third Cantor set, this is new and significant. The
middle-third Cantor set is one of the fractals which does not have a Fourier
basis. Many others do!
(A sample of researchers connected to the FRG and with papers on the subject:
Palle Jorgensen, Steen Pedersen, Yang Wang, Jeff Lagarias, Izabella Laba,
Alex Iosevich, Terence Tao,... A sample of papers as of May 15, 2003:
[B1]-[B14] below.)
Research on exact harmonic analysis-duality principles in geometric measure
theory are still in their infancy. But there is a lot of interest in this.
Note that R. Strichartz's NSF-funded undergraduate research projects have this
focus. We plan to continue to work with Strichartz and his team in this
direction.
This circle of problems around the Fuglede conjecture is not isolated. Don't
think of math as finite. Rather: "Infinite in all directions", is more like
it! We usually see that each answered question opens up three new questions.
That is especially true for the good problems in math. (Hmm...!, it would
sound like math is not efficient, but the good stuff is what we learn from
solutions to problems! Perhaps more so than the problems themselves.) Anyway
what we call "The Fuglede problem", or conjecture (I forgot when it was
elevated to a conjecture!) is in fact many problems..! A major theme in math
is that of understanding connections between geometry (for example tiling) and
some kind of spectrum. What I learned from the last wonderful
Terence Tao
paper, and papers of others,
is that it may be possible to do some kind
of functor from geometry to an "easier" setup (finite combinatorics and
algebra) involving only certain finite cyclic groups G. When is this is
successful? If the assignment is a functor! We have to be able to get an
implication like this: Within the spectral setting coming from a suitable
Hadamard matrix, verify the implication: "No solution in the finite case (a
particular Gd for some d)" implies "no solution to the original problem!"
The original problem here is the tiling question. Looked at this way, we are
just scratching the tip of an ice-berg.
[B1]
D. Dutkay, P. Jorgensen,
Wavelets on fractals, preprint June 2003, Univ. of
Iowa, submitted to Revista Matemática Iberoamericana.
[B2]
B. Fuglede, Commuting self-adjoint partial differential operators and a
group-theoretic problem, J. Funct. Anal. 16 (1974), 101-121.
[B3]
A. Granville, I. Laba, Y. Wang, On finite sets which tile the integers,
Preprint Dec 19, 2001.
[B4]
A. Iosevich, N. Katz, T. Tao, Convex bodies with a point of curvature do not
have Fourier bases, Amer. J. Math. 123 (2001), 115-120.
[B5]
A. Iosevich, S. Pedersen, Spectral and tiling properties of the unit cube,
Internat. Math. Res. Notices 1998 (1998), no. 16, 819-828.
[B6]
P. Jorgensen, Spectral theory of finite-volume domains in Rn, Adv. in Math. 44
(1982), 105-120.
[B7]
P. Jorgensen, S. Pedersen, Spectral theory for Borel sets in Rn of finite
measure, J. Funct Anal. 107 (1992), 72-104.
[B8]
P. Jorgensen, S. Pedersen, Spectral pairs in Cartesian coordinates,
J. Fourier Anal. Appl. 5 (1999), 285-302.
[B9]
I. Laba, Fuglede's conjecture for a union of two intervals, Proc. Amer. Math. Soc. 129 (2001), 2965--2972.
[B10]
J.C. Lagarias, J.A. Reeds, Y. Wang, Orthonormal bases of exponentials for the
n-cube, Duke Math. J. 103 (2000), 25-37.
[B11]
J.C. Lagarias, Y. Wang, Tiling the line with translates of one tile, Invent.
Math. 124 (1996), 341-365.
[B12]
S. Pedersen, Y. Wang, Universal spectra, universal tiling sets and the
spectral set conjecture, Math. Scand. 88 (2001), 246--256.
[B13]
Y. Wang, Wavelets, tiling, and spectral sets, Duke Math. J. 114 (2002), 43--57.
[B14]
Y. Liu and Y. Wang, The uniformity of non-uniform Gabor bases, Adv. Comput. Math. 18 (2003), no. 2--4 (special issue on Frames edited by A. Aldroubi and Q. Sun), 345--355.
-
Problem C: Irregular Translations. The result
of Wang [Wan01] on admissible translation and dilation sets for wavelets
arising from wavelet sets shows that these sets can be irregular. The same
has not been studied for other type of wavelets.
What if we change the wavelet set condition to Meyer wavelets?
What about compactly supported wavelets and MRA wavelets?
Wang's approach
differs substantially from the approaches in [LWWW02] and [Füh01].
Could it be used to study the admissible dilation sets in a continuous wavelet
transform? How could an multiresolution analysis be defined with more than one
scaling factor? If so, will there be potential for new applications? The members
of the FRG have much combined expertise in areas related to wavelets,
wavelet sets, and irregular sampling. In particular, Larson was the first to
study wavelet sets, Aldroubi, Benedetto and Heil have extensive expertise in
irregular sampling and MRA wavelets, and Jorgensen and Ólafsson have
studied wavelets and wavelet sets from the point of view of representation
theory, which may offer another important insight into this problem.
[Füh01]
H. Führ, Admissible vectors for the regular
representation, Proc. Amer. Math. Soc. 130 (2002), no. 10, 2959-2970 (electronic).
[LWWW02]
R. S. Laugesen, N. Weaver, G. Weiss and E. Wilson,
A characterization of the higher dimensional groups associated with
continuous wavelets, J. Geom. Anal. 12 (2002), no. 1, 89-102.
[Wan01]
Y. Wang, Wavelets, tiling and spectral sets,
Duke Math. J. 114 (2002), no. 1, 43-57.
Project areas:
-
Wavelet sets: implementation and abstract wavelet theory (manager: L.W. Baggett).
-
Finite, Fourier, and Gabor frames: sampling and Beurling-Landau theory
(manager: C.E. Heil).
-
Spectral-tile duality in wavelet theory (manager: P.E.T. Jorgensen);
for details see the web site of Izabella Laba,
especially the section
Tilings of Rn and the
spectral set conjecture.
Participants:
| FRG member:
|
Specialties:
|
Grad students:
|
Akram Aldroubi
Vanderbilt University
|
Wavelets, frames, sampling theory, signal/image processing, biomedicine
|
Armando Rodado
|
Lawrence W. Baggett
University of Colorado
|
Harmonic analysis, representation theory, wavelets and generalized multiresolution analyses
|
Toby Fernsler
|
John J. Benedetto
University of Maryland
|
Classical harmonic analysis, frames and wavelet theory, sampling theory, speech compression, periodicity detection
|
Joseph Kolesar,
Alex Powell, and
Juan Romero
|
Christopher E. Heil
Georgia Institute of Technology
|
Time-frequency analysis, frames, pseudodifferential operators, MRA multiwavelets
|
Kasso Okoudjou
|
Palle E.T. Jorgensen
University of Iowa
|
Operator theory, spectral theory, spectrum-tile duality, qubit algorithms, mathematical physics, symbolic dynamics
|
Dorin Dutkay and
Paul Johnson
|
David R. Larson
Texas A&M University
|
Operator algebras, operator theory, wavelets, frames, functional analysis, applied harmonic analysis
|
Troy Henderson and
Scott Armstrong
|
Gestur Ólafsson
Louisiana State University
|
Harmonic analysis and representation theory, special functions, orthogonal polynomials
|
Troels Johansen and
Imitiaz Hossain
|
Yang Wang
Georgia Institute of Technology
|
Self-similarity, tiling, fractal geometry, spectral sets, wavelets
|
|
Events (upcoming events in red):
|
FRG-meetings, workshops, consultations, and collaborations: |
| July 1-7, 2002 |
University of Colorado, Boulder
Workshop: L. Baggett, P. Jorgensen, K. Merrill, J. Packer: "Tiling theory, spectral sets, and the Fuglede Conjecture." Research for the paper
"Transitive actions of groups of unitary matrix functions on resolution subspaces of L2(Rd) with multiple generators" |
|
| July 12-21, 2002 |
Workshop:
"Tiling theory, spectral sets, and the Fuglede
conjecture".
Organizer, David R. Larson
Location:
Texas A&M University
Ten-day workshop |
Problems discussed
|
| October 2002 |
Vanderbilt University
Five-day workshop
Postponed. Details and dates to be announced. |
|
| January 19-21, 2003 |
Workshop II:
"Modulation spaces and the continuous
wavelet transform".
Organizer, J. Benedetto.
Location: University of Maryland,
College Park.
--The dates for the
UMD workshop, immediately following the
2003 Annual Meeting of the AMS
(Baltimore, January 15–18, 2003):
Sunday, January 19, 2003, afternoon session;
Monday, January 20, 2003 (MLK Holiday), morning and afternoon sessions;
Tuesday, January 21, 2003, morning session.
For information on the Special Session on
Wavelets, Frames and Operator Theory
organized by C. Heil, P. Jorgensen, and D. Larson
at the 2003 Annual Meeting of the AMS,
click here.
|
|
| March 12-16, 2003 |
Workshop III:
"Modulation spaces, wavelet sets, and the Fuglede conjecture".
Organizer, G. Ólafsson.
Location: Louisiana State University,
Baton Rouge.
Five-day workshop
on Wavelets and Frames, prior to the
AMS sectional meeting
(Baton Rouge, March 14-16, 2003)
--The dates for the
LSU workshop, before and during the
2003 Spring Southeastern Sectional Meeting
of the AMS
(Baton Rouge, LA, March 14–16, 2003):
Wednesday, March 12, 2003, morning and afternoon sessions;
Thursday, March 13, 2003, morning sesstion, noon FRG meeting, and afternoon discussion;
Friday, March 14-Sunday, March 16, 2003, the workshop becomes a part of the Special Session on Frames, Wavelets, and Tomography at the AMS meeting in Baton Rouge.
For information on the Special Session on
Frames, Wavelets, and Tomography
organized by G. Ólafsson
at the AMS Sectional Meeting, Baton Rouge, March 14-16, 2003,
click here. |
|
| May 11-13, 2003 |
Workshop:
"The Fuglede conjecture and Gabor frame theory".
Organizer, Akram Aldroubi
Location:
Vanderbilt University, Nashville, TN
Three-day workshop
Tutorial 1: "Excess and density of frames", Chris Heil.
Tutorial 2: "Fuglede
conjecture or related topics", Yang Wang.
Tutorial 3: "Fuglede conjecture", Palle Jorgensen and Steen Pedersen.
Problem sessions: Participant can present problems they wish to discuss.
Collaborative research; Group can form and small seminar rooms
will be available for groups who wish to discuss possible new
collaborations or continue ongoing collaborations.
Following the workshop, there is International
Conference on Advances in Constructive Approximation, Nashville, May
14-17, 2003 (John
Benedetto will be giving one of the main talk at this conference).
|
|
| June 23 - July 2, 2003 |
Workshop: "Three wavelet themes".
Organizer, Lawrence Baggett.
Location: University of Colorado, Boulder
Ten-day workshop
Theme 1: "Wavelet sets, and techniques for their construction", L.
Baggett, J. Benedetto, and K. Merrill.
Theme 2: "Modulation spaces", C. Heil.
Theme 3: "Wavelet frames on irregular grids and nonharmonic Gabor
systems", A. Aldroubi.
These tutorials, listed below as three-hour blocks, will of course
include breaks when needed. There will also be ample time for subsets
of participants to work together on private projects, and some people
may wish to give more formal talks. These will be arranged during the
workshop.
Monday June 23:
9am - noon, Theme 1.
2pm - 5pm, Theme 2.
6pm: Party at Larry and Christy's. (Directions later.)
Tuesday June 24:
9am - noon, Theme 1.
2pm - 4pm, Theme 2.
4pm-5pm: Brief summaries of selected FRG projects.
5pm - 6pm, meeting of the FRG members with Joe Jenkins.
Wednesday June 25:
9am - noon, Theme 1.
2pm - 5pm, Theme 2.
Thursday June 26:
9am - noon, Theme 3.
2pm - 5pm, Theme 3.
Friday June 27:
9am - noon, Theme 3.
2pm - 5pm, Contributed talks (TBA).
Saturday and Sunday June 28 and 29, free time. Private projects, extra
talks, hiking, touring,...
Monday June 30:
Revisit theme 1, discussions, problem sessions, other talks.
Tuesday July 1:
Revisit theme 2, discussions, problem sessions, other talks.
Wednesday July 2:
Revisit theme 3, discussions, problem sessions, other talks.
Participants:
Alex Powell,
Ed Wilson,
Guido Weiss,
Keri Kornelson,
Gestur Ólafsson,
Pete Casazza,
Palle Jorgensen,
Eric Weber,
John Benedetto,
Judy Packer,
Radu Balan,
Brad Ulrich,
Casey Leonetti,
Juan Romero,
Marcin Bownik,
Ozgur Yilmaz,
Wayne Lawton,
Wojtek Czaja,
Akram Aldroubi,
Dorin Dutkay,
Matt Fickus,
Chris Heil,
Kathy Merrill,
David Larson,
Yang Wang,
Vera Furst,
Kasso Okoudjou,
Norbert Kaiblinger,
Francois Meyer,
Steen Pedersen,
Jim Daly,
Keith Phillips,
Josip Derado,
Brody Johnson.
|
|
| October 11-14, 2003
|
Workshop: " ".
Organizers, Christopher E. Heil, Yang Wang.
Location: Georgia Tech
Tentative schedule:
Saturday, Oct. 11: 2:00-4:00 Tutorial by Yuesheng Xu.
Sunday, Oct. 12: 9:30-12:00 Tutorial by Guowei Wei;
3:00-5:00 Tutorial by Guowei Wei.
Monday, Oct. 13: 9:30-12:00 Tutorial by Gestur Ólafsson;
3:00-5:00 Tutorial by Gestur Ólafsson.
Tue, Oct 14: 9:30-12:00 Tutorial by Yuesheng Xu.
Participants:
Lawrence Baggett,
Eugene Belogay,
Bernhard Bodmann,
Dorin Dutkay,
Vera Furst,
Bin Han,
Deguang Han,
Palle Jorgensen,
Keri Kornelson,
Mark Lammers,
Gestur Ólafsson,
Manos Papadakis,
Darrin Speegle,
Qiyu Sun,
Guowei Wei,
Victor Wickerhauser,
Yuesheng Xu,
Ozgur Yilmaz,
and local Georgia Tech people:
Xinrong Dai,
DJ Feng,
Jeff Geronimo,
Christopher Heil,
Christian Houdré,
Norbert Kaiblinger,
Sandie Leach,
Becky Upchurch,
Yang Wang,
Long Wang,
Hao Min Zhou.
|
|
| February 15-21, 2004 |
Miniworkshop:
"Wavelets and Frames".
Location:
Mathematisches Forschungsinstitut Oberwolfach, Lorenzenhof, Oberwolfach-Walke, Germany.
Organizers:
Hans G. Feichtinger, Professor,
Institute of Mathematics, University of Vienna,
hans.feichtinger@univie.ac.at;
Palle E.T. Jorgensen, Professor,
Department of Mathematics, The University of Iowa,
jorgen@math.uiowa.edu;
Dave Larson, Professor,
Department of Mathematics, Texas A&M,
larson@math.tamu.edu;
Gestur Ólafsson, Professor,
Department of Mathematics, Louisiana State University,
olafsson@math.lsu.edu.
|
Workshop introduction
Duality principles in analysis
|
| Spring 2004 |
Workshop.
Organizer, Palle E.T . Jorgensen
Location:
University of Iowa, Iowa City, IA
In a slight abuse of geography, this workshop was subsumed in the Oberwolfach miniworkshop above.
|
|
| July 2004 |
Workshop:
" ".
Organizer, J. Benedetto.
Location: University of Maryland,
College Park.
Ten-day workshop |
|
| Fall 2004 |
Workshop:
" ".
Organizer, G. Ólafsson.
Location: Louisiana State University,
Baton Rouge.
Workshop |
|
| Spring 2005 |
Workshop:
" ".
Organizer, Akram Aldroubi
Location:
Vanderbilt University, Nashville, TN
Workshop |
|
|
Meetings and conferences where one or more members of this NSF Focused Research Group is an organizer or a speaker: |
5th Joint IDR-IMA Workshop
April 9-13, 2001
|
Organizers: Ronald DeVore, Amos Ron, Patrick Van Fleet.
Location: Institute for Mathematics and its Applications (IMA), University of Minnesota, Minneapolis
Abstracts: Aldroubi,
Heil,
Jorgensen,
Larson.
Pictures of
Jorgensen
and Larson speaking
and in the audience. |
AMS Meeting #982
November 9-10, 2002
|
AMS Special Session: Functional and Harmonic Analysis of Wavelets, Frames and Their Applications.
Organizers: D. Han and M. Papadakis.
Location: University of Central Florida |
AMS Meeting #983: the
annual AMS winter meeting
January 15-18, 2003
|
AMS Special Session:
Wavelets, Frames and Operator Theory.
Organizers: C. Heil, P. Jorgensen, and D. Larson.
Location: Baltimore, Maryland
|
AMS Meeting #984
March 14-16, 2003
|
AMS Special Session:
Frames, Wavelets and Tomography.
Organizer: G. Ólafsson.
Location: Louisiana State University, Baton Rouge, LA
|
| June 15-22, 2003 |
European Conference: Functional Analysis VIII
Location: Dubrovnik, Croatia
"Functional Analysis VIII" is a conference and a postgraduate school on
functional analysis, and related fields, with several more or less independent
parts dealing with various aspects of functional analysis (operator algebras,
probability theory, harmonic analysis, wavelets, representation theory...).
The program will include series of lectures, single lectures and short
communications.
The conference will be held in Dubrovnik, June 15-22, 2003 at the
"Inter-University Centre". This will be the eighth meeting; the first seven
were held in 1981, 1985, 1989, 1993, 1997, 1999 and 2001. Most of the main
lectures were published in Springer Verlag Lecture Notes (issues 948 and 1242)
and in Various Publication Series of the Aarhus University (issues 40, 43, 44
and 45).
The organizers are: Hrvoje Kraljevic, Davor Butkovic, Murali Rao, Damir
Bakic, Pavle Pandzic, Hrvoje Sikic and Zoran Vondracek.
Some of the invited plenary speakers:
Palle T. Jorgensen, Univ. of Iowa, USA; Bojan Magajna, Univ. of Ljubljana,
Slovenia; Vladimir M. Manuilov, Moscow State Univ., Russia; Klaus Thomsen, Univ.
of Aarhus, Danmark; J.D. Maitland Wright, Univ. of Reading, UK; Dubravka Ban,
University of Split, Croatia and Southern Illinois University, Carbondale, USA;
Peter Bantay, Eötvös Lorand Univ., Budapest, Hungary; Dan Barbasch, Cornell
University, USA; Corinne Blondel, University Paris 7, France; Mladen Bozicevic,
University of Zagreb, Croatia; William Casselman, University of British
Columbia, Canada; Henry Kim, Univ. of Toronto, Canada; Atsushi Matsuo, Dept. of
Math. Sciences, Univ. of Tokyo, Japan; Dragan Milicic, University of Utah, USA;
Allen Moy, HKUST, Hong Kong, China; David Vogan, M.I.T., USA; David R. Larson,
Texas A&M University, USA; Darrin Speegle, Univ. of St. Louis, USA
Part of the Program:
Monday, June 16, 2003
8:45-9:00 Opening ceremony 9:00-9:45 D.R.Larson Operators, wavelets and frames
I ..............
Tuesday, June 17, 2003
9:00-9:45 P.E.T. Jorgensen Some connections between operator theory and
wavelet analysis I
9:55-10:40 D.R. Larson Operators, wavelets and frames II
11:00-11:45 D. Speegle Wavelet constructions in Rn I ............
Wednesday, June 18, 2003
9:00-9:45 W. Schachermayer Optimal investment strategies in incomplete
financial markets III ................
Thursday, June 19, 2003
15:10-15:55 P.E.T. Jorgensen Some connections between operator theory and
wavelet analysis II
Friday, June 20, 2003
9:55-10:40 P.E.T. Jorgensen Some connections between operator theory and
wavelet analysis III
11:00-11:45 D. Barbasch The role of unipotent
representations in the classification of the unitary dual of a reductive group
III .............
Saturday, June 21, 2003
9:55-10:40 P.E.T. Jorgensen Some connections between operator theory and
wavelet analysis IV
11:00-11:45 D.R.Larson Operators, wavelets and frames IV
................
|
| May 24-30, 2004 |
Second International Conference on Computational Harmonic Analysis in conjunction with the 19th Annual Shanks Lecture Honoring Baylis and Olivia Shanks:
conference web page (or see the Wavelet Digest announcement).
Organizers: Akram Aldroubi, Charles Chui,
Emmanuelle Candes, Richard Baraniuk, Francois Meyer, Thomas Strohmer, Hamid Krim, Bruno Torresani,
Douglas Hardin, Ed Saff.
Location: Vanderbilt University, Nashville Tennessee.
Abstract of Jorgensen's talk
|
Reports:
First annual report (June 2003)
|