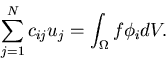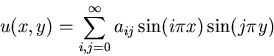22M:176 Finite Elements
Programming Assignment (Assignment #3)
Due Wednesday, December 9th, 1998
In this assignment we will build a simple FEM solver for two-dimensional
PDE's of the form
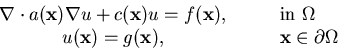
We will use MATLAB to solve the system of equations, and the triangulation
will be provided.
We will use piecewise linear basis functions under the given triangulation.
The basis function 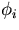 is the piecewise linear function which is one at vertex
is the piecewise linear function which is one at vertex 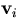 of the triangulation, and zero at all other vertices of the triangulation.
of the triangulation, and zero at all other vertices of the triangulation.
So, our purpose is to define the system of linear equations to solve.
We will need to compute the integrals
![\begin{displaymath}\begin{array}{c}\displaystyle \int_\Omega[a\nabla\phi_i\c... ...phi_j] dV,\\ \displaystyle \int_\Omega f \phi_i dV.\end{array}\end{displaymath}](img4.gif)
To approximate these integrals we will use the following quadrature formula
for a triangle K with vertices 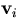 ,
i=1,2,3:
,
i=1,2,3:
![\begin{displaymath}\int_K h dV \approx \vert K\vert\left[ \frac1{20}\sum_i h({... ...um_{i,j:i<j}h({\bf v}_{ij}) +\frac9{20}h({\bf v}_{123})\right]\end{displaymath}](img5.gif)
where 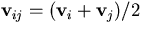 ,
,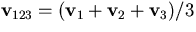 ,
and |K| is the area of triangle K.
,
and |K| is the area of triangle K.
Data structures
Perhaps the most complex part of the coding is organizing the data in an
efficient way. MATLAB has sparse matrices, which you should use for storing
the linear equations.
The triangulation will be represented by a collection of arrays as follows:
Suppose that there are N nodes (including both internal and
boundary nodes) and M triangles.
-
vertex: This will be an
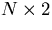 array of real numbers where vertex(i,1) is the x-component
of
array of real numbers where vertex(i,1) is the x-component
of 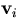 ,
and vertex(i,2) is its y-component.
,
and vertex(i,2) is its y-component.
-
triangle: This will be an
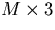 array of integers where triangle(j,1), triangle(j,2),
and triangle(j,3) are the indexes of the vertices of the triangle
Kj.
array of integers where triangle(j,1), triangle(j,2),
and triangle(j,3) are the indexes of the vertices of the triangle
Kj.
-
interior: This is an N component array of integers; interior(i)
is 1 if
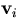 is an interior node and zero if it is a boundary node.
is an interior node and zero if it is a boundary node.
-
triang1 and next_triang: These two arrays give an efficient
way of determining which triangles touch a given vertex. triang1
is an N component array where triang1(i) is the index (in
next_triang)
of the ``first'' triangle touching vertex
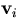 .
next_triang
is a two-column array which translates the entries in triang1
to indexes into triangle, as well as giving the index (into next_triang)
of the following triangles touching
.
next_triang
is a two-column array which translates the entries in triang1
to indexes into triangle, as well as giving the index (into next_triang)
of the following triangles touching 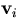 .
Here is some MATLAB code to process all triangles touching vertex
.
Here is some MATLAB code to process all triangles touching vertex 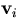 :
:
% Find all triangles touching vertex # i
tri_index = triang1(i);
while tri_index > 0
k = next_triang(tri_index,1);
% Process triangle # k
..... triangle(k,1) ....
tri_index = next_triang(tri_index,2);
end
These arrays will be computed by a routine mk_nxt_tri.
For computing integrals involving 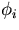 ,
we need to find all of the triangles K that touch
,
we need to find all of the triangles K that touch 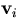 .This
can be done using the above code. For computing
.This
can be done using the above code. For computing
![\begin{displaymath}\int_\Omega[a\nabla\phi_i\cdot\nabla\phi_j+c\phi_i\phi_j] dV\end{displaymath}](img10.gif)
we should only integrate over only the triangles that touch
both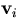 and
and 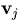 .Since
each vertex is touched by only six or so triangles, we can test each triangle
as we find it using the above code:
.Since
each vertex is touched by only six or so triangles, we can test each triangle
as we find it using the above code:
% Find all triangles touching vertex # i and vertex # j
tri_index = triang1(i);
while tri_index > 0
k = next_triang(tri_index,1);
if triangle(k,1) == j | triangle(k,2) == j | triangle(k,3) == j
% Integrate over triangle # k
..... triangle(k,1) ....
end
tri_index = next_triang(tri_index,2);
end
How do we find |K|?
The area of a triangle K with vertices 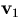 ,
, 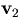 and
and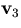 can be computed as
can be computed as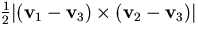 where
where 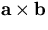 is the vector cross product. Alternatively, if
is the vector cross product. Alternatively, if 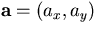 in co-ordinate form,
in co-ordinate form,
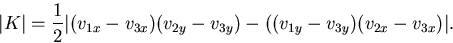
since 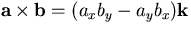 where
where 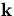 is the unit vector in the ``z'' direction.
is the unit vector in the ``z'' direction.
Boundary conditions
When you formulate the Galerkin equations to solve, write
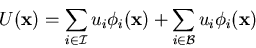
where 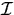 is the set of interior nodes and
is the set of interior nodes and 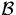 is the set of boundary nodes. If
is the set of boundary nodes. If 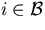 ,
make the i'th equation just
,
make the i'th equation just 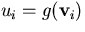 .For
.For 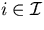 ,
the i'th equation should be the usual equation:
,
the i'th equation should be the usual equation:
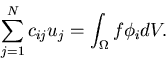
Test problem
We will have two test problems. The first will be to solve the Poisson
equation 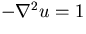 on the unit square
on the unit square 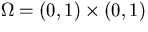 with homogeneous Dirichlet boundary conditions (u=0 on
with homogeneous Dirichlet boundary conditions (u=0 on 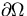 ).
For comparison purposes, the exact solution is
).
For comparison purposes, the exact solution is
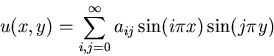
for suitable coefficients aij. Find the correct coefficients
for this problem.
The triangulation to use is the regular triangulation described in Q.3
or the 2nd assignment. Use 11 grid points on each axis.
The second test problem will be defined by the data in the ASCII files
vertex,
triangles,
triang1, and next_tri which contain the data for the
corresponding arrays. These are available via the
WWW page . The mesh described by the above files looks like this:
ap_mesh.pdf
David Stewart
11/18/1998
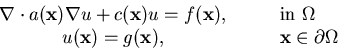
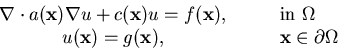
![]() is the piecewise linear function which is one at vertex
is the piecewise linear function which is one at vertex ![]() of the triangulation, and zero at all other vertices of the triangulation.
of the triangulation, and zero at all other vertices of the triangulation.
![\begin{displaymath}\begin{array}{c}\displaystyle \int_\Omega[a\nabla\phi_i\c... ...phi_j] dV,\\ \displaystyle \int_\Omega f \phi_i dV.\end{array}\end{displaymath}](img4.gif)
![\begin{displaymath}\int_K h dV \approx \vert K\vert\left[ \frac1{20}\sum_i h({... ...um_{i,j:i<j}h({\bf v}_{ij}) +\frac9{20}h({\bf v}_{123})\right]\end{displaymath}](img5.gif)
![]()
![]()
![]()