22M:176 Finite Elements
Assignment 1
Due Monday, 28th September, 1998

1.

Quadratic elements in one dimension. Consider the following quadratic basis functions:

$$\begin{array} {c} \phi_i(x) = \left\{\begin{array} {ll} 2(... ...{i+1}\ 0,& \mbox{otherwise} \end{array}\right.. \end{array}$$

The grid spacing x_i+1-x_i=h=1/N. Compute the stiffness matrix for the quadratic basis functions:

$$\begin{array} {r@{}l} c_{i,i} &{}= \int\phi_i'(x)^2 dx\ c... ...\ c_{i,i+1} &{}= \int\phi_i'(x)\phi_{i+1}'(x) dx \end{array}$$

Set up the stifness matrix and right-hand side for solving $u^{\prime\prime} = f(x)$ on the interval (0,1) with boundary conditions u(0)=u(1)=0 with N-1=9 interior equally-spaced grid points with f(x) = exp(-3x). Use Simpson's rule to approximate $\int\phi_i(x)f(x) dx$ and $\int\phi_{i+1/2}(x)f(x) dx$.

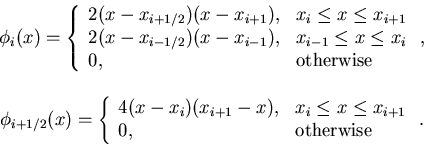
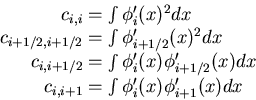
Solve the same differential equation using piecewise linear basis functions with half the grid spacing (i.e., with h=1/(2N)).

Given that the exact solution is u(x) = (1/9)(e^-3x+(1-e^-3)x-1), compute the error in your solutions. How do you compare the results of the two methods? Which is more accurate for the amount of computational work involved?

2.

Consider the cantilever beam problem

$$(\kappa(x) u^{\prime\prime})^{\prime\prime} = f(x)$$

where f(x) is the load on the beam. The variational form of the problem is to minimize

$$\int_0^L \frac12\kappa(x) (u^{\prime\prime})^2 dx$$

over all u(x) where u(0)=u'(0)=0. The essential (forced) boundary conditions are that u(0)=u'(0)=0. Find the remaining two natural boundary conditions (at x=L). [Hint: Start from the variational form.]

To set up a finite element method for this problem we need basis functions $\phi_i(x)$ for which $\phi_i'(x)$ is absolutely continuous. To set up such a basis, let

$$\psi(x) = \left\{\begin{array} {ll} 2x^2/3,&0\le x\le 1\ ... ...3,&1\le x\le 2\ 2(3-x)^2/3,&2\le x\le 3 \end{array}\right..$$

For a uniformly spaced grid, x_i=i L/N=i h (h=L/N), let $\phi_i(x) = \psi((x-ih)/h)$.

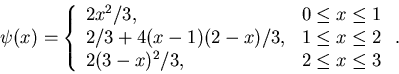
Show that $\phi_i(0)=\phi_i'(0)=0$ for $i=0,1,2,\dots,N-1$. Suppose that $\kappa(x)$ is the constant k. Compute the stiffness matrix: $c_{ij} = \int_0^L k \phi_i^{\prime\prime}(x)\phi_j^{\prime\prime}(x) dx$. [Hint: c_ij=0 unless i and j differ by less than 3. Also, be careful of the integrals with i or j close to N because of the limit x=L for the integral.]

Set up the equations to solve for u_i in our approximate solution

$$U(x) = \sum_{i=0}^{N-1} u_i \phi_i(x).$$

3.

(Cauchy's inequality) Here we prove that

$$\int f(x) g(x) dx \le \left[\int f(x)^2 dx\right]^{1/2} \left[\int g(x)^2 dx\right]^{1/2}.$$

Expand $\int (f(x)+\alpha g(x))^2 dx$ as a function of $\alpha$. Show this function is a quadratic in $\alpha$. Since $\int (f(x)+\alpha g(x))^2 dx\ge0$ for all $\alpha$, how many real roots can there be of this quadratic? Use this to show the result.

Also check the case $g(x)\equiv0$.